Джва года ждал этот тред!
По какой причине Бурбаки относились к теории категорий недружественно?
Почему недружественно? Откуда такая инфа? Картан вместе с Эйленбергом пилили гомоалгебру и вовсю там жонглировал функторами, а Гротендик так вообще в них души не чаял. Современный алтоп без категорий - вообще нонсенс.
Бытует легенда, что категории понадобились лишь для того, чтобы определить функторы, а фукнторы - чтобы ввести естественные преобразования. Так что как бы там ни было, функторы - это уже практически категории, как независимость интеграла от пути - гомологии. Тем более, что в "Гомологической алгебре" Картана-Эйленберга есть явные ссылки на понятие категории в смысле Маклейна-Эйленберга.
Тоже хочу рисовать такие картинки! Что читать, чтобы научится?
Голдблатт - Топосы. Категорный анализ логики.
На случай, если в будущих билдах GHC завезут очередную ковариантную ахинею, мне будет в неё легче вкатиться.
Да и на самом деле, ничего серьёзнее Категорий для Работающего МатемашЫна я так до сих пор и не прочитал.
Мне ваши Гротенфрики и Эйленбергерги как-то по барабану, если чё.
И сильно ли тебе помогли "категории для работающего"? Мне правда интересно, как вы используете это всё в своих хачкелях и что мешает пользоваться хачкелем без всего этого.
Авотхуйзнает. На топосах точно нет? Я чет в этих логиках и топосах не особо как-то вообще.
Ничего не мешает. Он же ответил вроде достаточно ясно: завезут в следующей версии гхц какую-нибудь очередную фишку - и сиди, разбирайся, что это за хуйня и что она значит. А ечли есть фундамент, то это как-то проще.
Но для написания кода на х-ле разбираться в этом необязательно, конечно.
А как связаны топосы и интуиционистская логика? Какую хошь логику такую на них и строй.
На самом деле, я не то что хочу любым способом доебаться, если что, просто мне правда сложно представить себе, что такое может быть в ЯП, что требует привлечения таких своеобразных математических структур, как категории. В явном виде, а не в духе подразумеваемых фон неймановских архитектур, булевых алгебр или чего-то ещё такого. Ну и в действительности я почти не знаком с хачкелем но знаком с быдлокодерством на иных языках в целом.
Интересный тред. Спасибо.
И что? Интерес в хаскель-коммунити к ТК не обусловлен какой-то острой необходиомстью для нужд понимания/использования хаскеля. Это сопутствующий интерес, сложившийся исторически.
Не совсем. В алтопе используется лишь некоторое подмножество категорного аппарата. Во всяких введниях в гомоалгебры и симплициальные гомологии категории излагаются довольно куце, в виде "наивной теории категорий" (определение, что такое категория, функтор, бла-бла-бла), не затрагивая такие вещи, как лемма Йонеды или аджойнты, например. Теория категорий всё ещё интересна в более общем сеттинге, чем топология и не ограничивается только ею (включая алгебру вообще, даже какие-то там основания).
Ну таки аджойнты как раз из топологии пошли. Но я тоже против того, чтобы редуцировать котягории только до гом. алгебры. В тех же топосах понаделано не меньше.
Является ли пустое множество стрелкой/морфизмом в ней?
Рассмотрим три множества A, B и С. И две стрелки f: A -> B, g: B -> C (стрелки тут это множества пар). Возможно же, что g ∘ f это пустое множество, если в B нет таких элементов, которые встречаются и в f, и в g. Но композиция должна быть стрелкой.
Для справки если что:
https://ncatlab.org/nlab/show/Rel
https://en.wikipedia.org/wiki/Category_of_relations
Является. Композиция с любым другим отношением пуста.
расходимся, теория категорий не нужна!
Нахуй нужны модули над кольцом вообще?
Довольно бессмысленная структура, никогда особо не мог понять, нахуй она нужна, исключая конечно тот вариант, когда кольцо это поле.
https://en.wikipedia.org/wiki/Mitchell's_embedding_theorem
>>5759
> Нахуй нужны модули над кольцом вообще?
проиграл
ncatlab нам построит мониматюку на топосах, будете ещё, картохи, диффуры как суб-infty-группоиды мыслить.
А ещё, как минимум, на дуализацию, из которой вырасли алгебры Хопфа и квантовое группы, не похуй.
Нахуй нужно что-то, кроме модулей над кольцом, вообще?
>как будтно на теорию категорий кому-то не поебать, если бы не абелевы и производные категории
Кстати, а зачем нужны производные категории? Ну, можно все производные функторы записать сразу как один, можно композицию оных без спектралки написать, ну и что? Где это реально помогает? У вербита и ко, когда они обсуждали, что надо знать в математике (я говорю про более ранние обсуждения, не сегодняшние), всё время проскальзовало, что без этих категорий никуда. Но где никуда-то? Что с этим делать? Всё равно же производные функторы считаются по одному через точные последовательности. Так зачем они?
Не говори только, мол, типа как в геометрии, можно локально рассматривать, можно глобально, и типа локально это зашквар, а глобально заебись. Всё это хуйня. Что они действительно дают, эти категории?
ну например D^b(Coh(X))
аргумент не в том, что это более правильный формализм для производных функторов, аргумент, что это важный инвариант многообразия
кузнецов-орлов-бондал вон кучу понаоткрывали вещей, которые можно в ней увидеть. с ходу --- промежуточные якобианы.
гомологическая зеркальная симметрия формулируется в терминах эквивалентности триангулируемых категорий, одна из которых D^b(Coh(X))
извращённые пучки живут в ней, извращённые пучки нужны для того, чтобы обобщить соответствие римана-гильберта с плоских связностей на векторных расслоениях на голономные д-модули
А как думаешь, это естественный формализм или ad-hoc? Просто таким костылём всё это кажется - пиздец.
ну нет, как раз-таки описывать производные функторы на производных категориях канонiчней
понятно, что это всего лишь язык, но на этом языке проще говорить
потому что не делается например акцент на резольвентах. просто вот мы формально обратили квази-изоморфизмы комплексов и задались вопросом: как нам продлить функтор с объектов на такую категорию?
типичный пример понижения концептуальной сложности: спектралка гротендика. в классическом формализме этот результат надо формулировать именно что с использованием спектралки. с производными категориями ты просто говоришь, что при наличии достаточного количества инъективных объектов, если F-acyclics посылаются в G-acyclics, то R(G \circ F) = RG \circ RF.
понятно, что начни ты выписываеть это через конкретные резольвенты, у тебя всё равно получится спектралка. но тут ситуация как с безкоординатными рассуждениями с линейной алгебре против рассуждений, когда ты всё определёшь в базисе и потом доказываешь, что ничего от выбора базиса не зависит.
ну или вот: двойственность серра тоже на производных категориях формулируется естественней. двойственность серра можно сформулировать как постоение сопряжённого функтора к f_*: D^b(X) \to D^b(Y), его называют f^! обычно. так вот делинь показал (статья называется как-то типа "Cohomologie a supports propres et чтототам"), что этот сопряжённый существует по каким-то почти тавтологическим причинам. это уже когда ты начинаешь вычислять его на проективном гладком многообразии у тебя вылезает \omega в качестве дуализируещего комплекса, а так двойственность существует в гораздо большей общности. понять это, глядя в утверждение двойственности с \omega, представляется невозможным.
тут циклическое определение: "гомотопическая алгебра" это название статьи квиллена, где он прописал определение модельных категорий.
насчёт модельных категорий у меня короче нету мнения. дело в том, что это лишь один из зоопарка формализмов (a_\infty, DG, дериваторы), которые нужны в "производной геометрии", что бы это ни значило. было бы натяжкой говорить, что эти формализмы вошли в арсенал среднего работающего математика (в отличие от производных категорий), а поскольку прям эти вещи я не изучал, являются ли модельные категории ответом на все вопросы, сказать не могу.
есть пара сюжетов более старых, классических, где возникают, типа гомологий андрэ-квиллена и кокасательного комплекса иллюзи, и с целью их ровно понять модельные категории я бы выучил (выглядит вполне подъёмно), а вот DGA и эти все альтернативные формализмы.. это уже наука переднего края, она огромная, надо кучу времени убить, чтобы составить мнение.
у тебя ровно написано, что сингулярный комплекс Cone f определяется через самого себя. может ты что-то другое имеешь в виду?
 185 Кб, 1366x768
185 Кб, 1366x768Почему C.(CK)/C.(s) изоморфно cone(C.K), а не просто C.(CK)? какой в этом топологический смысл?
(CK - конус над топ. пространством, cone(K) - конус комплекса)
пусть f морфизм из K в L, как у вайбеля
подумай о такой симплициальной структуре на cone(f): i-симплексы это конусы над (i-1)-симплексами в К и i-симплексы в L
теперь сравни это с определением конуса морфизма на симплициальных цепных комплексах, индуцируемого f
Ребятки, сколько времени вам понадобилось для освоения самого основного теорката? Ну книжек типа Эводи, Маклейна и т.д. Не углубляясь во всякие энкатегории.
Есть куча универсальных конструкций:
representable functor
adjoint functor
limit/colimit
end/coend
Kan extension
dependent sum/dependent product
Ещё универсальный морфизм, хотя это и есть определение универсальной конструкции.
Так вот, всё это весело друг через друга выражается.
Они как-нибудь классифицируются? Ну то есть есть там какая-нибудь система? Или это пока слишком сложно и абстрактно.
Ну и у меня немного траблы с расширением кана через лимиты...
Вот обычно канонiческий и "один есть и норм". А носятся потому, что он очевиден в силу несвободы выбора каких-то условий или произвола, которые могут повлиять.
Предлагаю такой вопрос - для чего может потребовать коэкспоненциал?
Обозначим его как (Z_Y, coeval).
Это начальный универсальный морфизм из объекта Z в функтор ( - \times Y).
(можно также рассматривать вариант функтора: ( Y \times - ) )
в некотором элементарном топосе есть f:X->Y, и
пусть мы знаем, что индуцированный морфизм
f_preimage : (Y->2) -> (X->2)
- биективен.
Тогда f должен быть тоже биективен. Соответсвенно пытаюсь построить invf.
Но чет у меня получается построить только отображение ( f_preimage o i_Y):Y->(X->2). А надо invf:Y->X.
Жалко чёт меня игнорируют и тред пустоват. Чому так? Мне спрашивать в местном раковнике рядом с вопросами про вычисление производных?
Конкретно этот вопрос - уже не буду - там просто по универсальному свойству пуллбэка $2^X \times_2 1$
В чём сила presheaves on sites ?
Этальные когомологии и топология Гротендика?
Что почитать на эту тему для новичка?
И самый важный вопрос: С помощью этого получены ли сильные результаты, влияющие на большую часть математики?
>С помощью этого получены ли сильные результаты, влияющие на большую часть математики?
очень мудацкий вопрос. платиново мудацкий. фу такие вопросы задавать. нет, правда, анон, пойди, утопись в говне от стыда
Да знаю я, что мудацкий.
Похоже немного на то, когда спрашивают "А зачем ты этим занимаешься, кому это нужно?"...
Ну а вот если меня интересует мотивация перечисленных там конструкций? По-твоему о мотивации стыдно спрашивать?
(например пост https://2ch.hk/math/res/20.html#6723 (
Мне хотелось бы верить, что оно всё друг с другом связано и дико друг для друга полезно.
Но пока я вижу только изолированные друг от друга области.
Или ты имеешь в виду подобные вопросы как часть fast and loose reasoning style?
а твой вопрос попахивает чем-то типа "я хочу быть уверен, что этот
раздел самый важный, самый пиздатый, самый модный, правда, это так?"
во-первых, как я уже говорил, вопрос мудацкий. с какого хуя отвечающий
должен заботится о твоём душевном комфорте, и выступать тебе
оправданием, что интересующий тебя раздел самый лучший?
во-вторых, на такие вопросы ответ может быть только субъективным, что
в рамках анонимной борды делает его особенно мудацким
так, про мудацкость, надеюсь, достаточно разложил.
по существу: не очень понятно, что имеется в виду. "пучки на
сайтах". ну типа, когда ты определяешь этальные когомологии, то ты
конечно же работаешь с пучками на сайтах, этальные когомлогии это
производные функторы функтора глобальных сечений пучка на этальнм
сайте (так же как когерентные когомолгии есть производные функторы
функтора глобальных сечений пучка в обычном смысле, или на сайте
зариского). с другой стороны есть категорная логика, там тоже пучки на
сайтах, топосы и хуёпосы. целая книжка про это есть, мурдайка и
маклейна. если хочешь знать моё мнение, первое (эт. когомологии) ---
давно вошедший в обиход сюжет, рабочий инструмент, второе ---
маргинальное переливание из пустого в порожнее, что-то сродни
основаниям и теории множеств, с точки зрения работающего математика.
этальные когомологии, этальная топология конечно глубоко интегрированы
со многими разделами математики. например, с одной стороны есть
теорема сравнения, что этальные когомологии (проективного, кажется)
многообразия над C совпадают с сингулярными (ну там тонкость есть, как
это сформулировать: надо брать коэффициенты в Z/l^n Z, и брать
обратный предел, и тензорить с Q_l, в результате получится Q_l
векторное пространство, у которого размерность совпадает с
размерностью сингулярных H^*(X, R)), так что можешь смотреть на них
как на алгебраическое определение такой казалось бы топологическоей
штуки. более общо, этальная топология позволяет алгебраически
определять аналоги топологических инварианнтов. ну типа есть этальная
фунд группа, которая есть проконечное пополнение обычной (если
многобразие над C, опять же), есть вообще --- этальный проконечный
гомотопический тип.
с другой стороны, этальные когомологии можно считать не толко у
многообразий над C, можно у штук над числовым полем, например. тогда
на них действует абсолютная группа галуа. понять это действие --- в
каком-то смысле основной челлендж для теории чисел. можно работать над
конечным полем, тогда действует фробениус, есть формула следов
лефшеца, это используется например в доказательств гипотез Вейля.
можно считать этальные когомологии у колец целых числовых полей. это
вообще глючная тема, у Z оказываются когомологии как у 3-сферы. таким
образом можно думать про кольца целых числовых полей как про конечные
накрытия 3-сферы, про простые идеалы как про зацепления, там куча
аналогий. называется эта тема "arithmetic topology"
в общем куча всего. есть ещё алгебраические когомолгии де рама, так
вот можно доказывать теоремы сравнения этальных когомологий с ними, по
аналогии с тем, как есть сравнение между сингулярными и обычным де
рамом. есть ещё разложение ходжа на алгебраическом де раме, короче,
много происходит похоже на комплексные многообразия, но со своей
спецификой (действие галуа). большой кусок современной теории чисел
вокруг этого вертится (ключевые слова: п-адическая теория ходжа).
а твой вопрос попахивает чем-то типа "я хочу быть уверен, что этот
раздел самый важный, самый пиздатый, самый модный, правда, это так?"
во-первых, как я уже говорил, вопрос мудацкий. с какого хуя отвечающий
должен заботится о твоём душевном комфорте, и выступать тебе
оправданием, что интересующий тебя раздел самый лучший?
во-вторых, на такие вопросы ответ может быть только субъективным, что
в рамках анонимной борды делает его особенно мудацким
так, про мудацкость, надеюсь, достаточно разложил.
по существу: не очень понятно, что имеется в виду. "пучки на
сайтах". ну типа, когда ты определяешь этальные когомологии, то ты
конечно же работаешь с пучками на сайтах, этальные когомлогии это
производные функторы функтора глобальных сечений пучка на этальнм
сайте (так же как когерентные когомолгии есть производные функторы
функтора глобальных сечений пучка в обычном смысле, или на сайте
зариского). с другой стороны есть категорная логика, там тоже пучки на
сайтах, топосы и хуёпосы. целая книжка про это есть, мурдайка и
маклейна. если хочешь знать моё мнение, первое (эт. когомологии) ---
давно вошедший в обиход сюжет, рабочий инструмент, второе ---
маргинальное переливание из пустого в порожнее, что-то сродни
основаниям и теории множеств, с точки зрения работающего математика.
этальные когомологии, этальная топология конечно глубоко интегрированы
со многими разделами математики. например, с одной стороны есть
теорема сравнения, что этальные когомологии (проективного, кажется)
многообразия над C совпадают с сингулярными (ну там тонкость есть, как
это сформулировать: надо брать коэффициенты в Z/l^n Z, и брать
обратный предел, и тензорить с Q_l, в результате получится Q_l
векторное пространство, у которого размерность совпадает с
размерностью сингулярных H^*(X, R)), так что можешь смотреть на них
как на алгебраическое определение такой казалось бы топологическоей
штуки. более общо, этальная топология позволяет алгебраически
определять аналоги топологических инварианнтов. ну типа есть этальная
фунд группа, которая есть проконечное пополнение обычной (если
многобразие над C, опять же), есть вообще --- этальный проконечный
гомотопический тип.
с другой стороны, этальные когомологии можно считать не толко у
многообразий над C, можно у штук над числовым полем, например. тогда
на них действует абсолютная группа галуа. понять это действие --- в
каком-то смысле основной челлендж для теории чисел. можно работать над
конечным полем, тогда действует фробениус, есть формула следов
лефшеца, это используется например в доказательств гипотез Вейля.
можно считать этальные когомологии у колец целых числовых полей. это
вообще глючная тема, у Z оказываются когомологии как у 3-сферы. таким
образом можно думать про кольца целых числовых полей как про конечные
накрытия 3-сферы, про простые идеалы как про зацепления, там куча
аналогий. называется эта тема "arithmetic topology"
в общем куча всего. есть ещё алгебраические когомолгии де рама, так
вот можно доказывать теоремы сравнения этальных когомологий с ними, по
аналогии с тем, как есть сравнение между сингулярными и обычным де
рамом. есть ещё разложение ходжа на алгебраическом де раме, короче,
много происходит похоже на комплексные многообразия, но со своей
спецификой (действие галуа). большой кусок современной теории чисел
вокруг этого вертится (ключевые слова: п-адическая теория ходжа).
Сейчас вот именно Sheaves in logic я и почитываю.
Жалко, что маргинальное.
Интересно же для общего развития: логики на топосах, семантика Крипке и внутренний язык Митчелла-Бенабу.
В этом приятно копаться, чисто чтобы говорить научиться на этом категорном. Видимо меня это интересует простопотому что я не получил пока нужного количества образования? Приятель мой, говорил про одногонаучрука, который этим занимается: "все сначала хотят к [нейм]" Значит, наверное это надо пройти, пока нравится. Или лучше сразу идти дальше, только вот куда? У меня своего чувства вкуса нет.
p.s. сорян, я не Х., я просто устал
да понятное дело приятно копаться в определениях, синтаксисе и вещах, которые не апеллируют к чему-то существенному, а потому сложному
это как семечки лузгать
>>7847
Да забей ты на этого элитиста, занимайся чем нравится. Пучки и топосы в логике тоже интересны, тем более если ты знаешь про Крипке. Интереса к топологии это не убавит, зачем сознательно ограничивать себя чем-то одним. Изучай вместе с алгебраической геометрией хоть феноменологию, хоть махаяну, а элитистов запрещающих это, посылай нахуй.
Не соскучишься с вами.
какие свободные аналогии!
задай себе вопрос: про что написал маклейн книгу? когда? имеет ли отношение его книга к категорной логике?
я тоже знаю про семантику крипке и топосы. и замечу, никому не запрещаю чем-то там интересоваться. просто указываю, что есть ошромный сложный мир помимо категорной логики, на случай, если кому-то неочевидно
ну и не забудем, что маклейн бох, и ему заранее кредит доверия. и он знает ту математику, для переформулировки которой понадобится теория категорий, катенорная логика, и чёрт с рогами. может себе позволить вольный поиск, его книгу попробуют (уже попробовали) прочитать, потому что маклейн.
когда же молодой студент вышечки, любящий копаться в формализме, не хочет идти учить алггем там, потому что влом и не вызывает немедленный выброс допамина, это совсем другая история
> Это пройдёт само, или мне надо совершать над собой усилие(даже
скорее насилие)?
ну это твой выбор, потакать своим слабостям или нет, и кто я такой,
чтобы говорить тебе, что делать?
просто даю информацию к размышлению, что есть широко известный
феномен: играться с формализмом, доказывать эквивалентность
определений, строить пустые абстракции, не основанные на примерах,
встречающихся в природе гораздо проще и приятней, чем непосредственно
пытаться понять какое-то сложное явление.
тут конечно нет чёткой границы, есть континуум. вообще, гротендик учит
нас, что правильно выбранные определения превращают теоремы в
тавтологии. но надо различать, когда ты ищешь правильное определение,
а когда переливаешь из пустого в порожнее. это навык, это вкус,
описать в двух словах не получится. в каком-то смысле это один из
обязательных скиллов математика, лучше всего, если у тебя перед
глазами есть живой пример работающего математика, у которого ты можешь
ему научиться.
Ну я как-то подразумевал, что тот, которому ты отвечаешь не является каким-то студентом "вышечки", а взрослым человеком, сознательно выбравшем математику уже в зрелом возрасте, поэтому меня возмутило. Если это студент такие вопросы спрашивает, то ссать в ебало ему надо, конечно, за такое.
я уже запутался какой анон тут кто, если кого обидел, типа, прошу прощения. подразумеваю, что если человек спрашивает что-то про обучение математике, то значит он крякает как студент, ходит как студент, значит, можно считать студентом. в любом случае, нежно лелеять своё увлечение основаниями, семантикой крипке, и топосами, при этом игнорировать остальную математику, и считать, что всё нормально, типа учусь математике, буду специалистом по топосам --- это патология, это вам кто угодно скажет.
Полный прообраз пересечения множеств f(A/\B) должен быть равен пересечению полных прообразов множеств (fA)/\(fB).
Построив кубик из соответсвующих пуллбэков я получил пуллбэка одной из диагональных "плоскостей" единственный морфизм h:(fA)/\(fB)->f(A/\B)
А как блджад, в обратную-то сторону строить?
Да чтоб её, разметка поехала... Там, где "f" - "f" со звёздочкой, inverse image.
Ахах, как же я в лужу сел - прообраз же сопряженный и слева и справа функтор в топосе, так что лимиты и колимиты сохраняются, а топологии индуцируются и коиндуцируются.
Не расстраивайся. Всё нормально.
Внезапно, понимание категорий помогает в написании действительно больших приложений, если язык поддерживает композицию функций ( не только хаскель, даже си шарп это может). С опытом приходит понимание, что лучше сразу и явно отделить отношения от логики, а такой уровень абстракции - это ж категории и есть.
Также выглядят большинство идиотов, носящихся со своими пучками, тапалогиями и гамалогиями. Как же заебал этот рак.
ну есть идиоты носящиеся, а кто-то пользуется
утверждение же про роль теорката в функциональном программировании ПОТОМУ ЧТО КОМПОЗИЦИЯ ФУНКЦИЙ, показывает, что говорящий не в курсе ни насчёт функционального программирования, ни насчёт роли в нём категорий
мимо-другой-хачкелеёб
Рак это как раз не осилившие пучки ебаноиды вроде тебя.
ну типа да, источник вдохновения
хотя вот недавно какой-то хаскелоёб вроде убедительно рассказал, что на данный момент нету строго определённой категории ("категории Hask"), к которой можно было бы применять теоркатные конструкции и получать концепты из хаскеля. есть какие-то тонкие причины, но короче просто типы, которые можно определить в хаскеле, не образуют категорию, в отличие от распространённого мнения (там сложность с тем, что считать морфизмами)
>есть какие-то тонкие причины
В интернете пишут, что из-за undefined и прочих _|_ (это тип, у которого нет значений, a la пустое множество) проблемы. Можно, вроде, взять какое-то подмножество языка и думать категорно о нём.
для формальной семантики отсутствие корректного определения это удар ниже пояса
для проведения аналогий оно конечно можно в такие детали как боттом не вникать
Я вообще не знал что такое "формальная семантика", у вики в энверсии на "semantics of logic" в которой какая-то философская вода об Органоне Аристотеля.
Двачую! Всякий должен проводить жирную демаркационную линию между математикой с теорией категорий и языком программирования Haskell.
Уж очень он напоминает пузырь, ну как доткомы.
Да пусть используют, конечно. Просто интересно было, как им это помогает. Пока я вижу, что помогает так же, как Иисус Нику Вуйчичу
Обоснуй теперь свою бурную реакцию
 5 Кб, 231x121
5 Кб, 231x121Господа, прав ли я, что для вывода
hom(X x Y, Z) ~ hom(X, Z^Y)
достаточно лишь чтобы были все экспоненты и все бинарные продукты.
И не нужен терминальный объект, который почему-то всё-таки входит в определение декартово замкнутой категории. Почему?
Док-во:
(<-) UMP exp: g |-> Lg
(->) UMP prod и прекомпозиция: Lg |-> eval o (Lg x id_Y)
то, что секция и ретракция - по тем же причинам
https://en.wikipedia.org/wiki/Cartesian_closed_category
есть ссылка
S. Soloviev. "Category of Finite Sets and Cartesian Closed Categories", Journal of Soviet Mathematics, 22, 3 (1983)
Где это можно откопать?
Без терминального объекта теряешь свойства Set
 40 Кб, 953x400
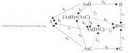
40 Кб, 953x400Вопрос: в каких категориях она верна?
Ведь если на диаграмме обратить все стрелки и заменить продукты на копродукты и наоборот, то получится тоже верная диаграмма.
Однако же обращённая диаграмма неверна в категории конечных множеств FinSet, у которой есть конечные лимиты и конечные колимиты!
Поэтому недостаточно просто существования произведений и дизъюнктивных объединений. Что ещё требуется?
Всё-таки наверное обращённая диаграмма верна и в FinSet, просто тогда единственный морфизм h_g - не изоморфизм.
А какое тогда свойство топоса конечных множеств заставляет морфизм h_g на изображенной прямой диаграмме быть изоморфизмом?
> Где это можно откопать?
http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=znsl&paperid=3401&option_lang=rus
Благодарю!
Zhen Lin утверждает, что произведение конечного числа эпиморфизмов - эпиморфизм.
Помимо этого, из множественной интуиции, кажется, что спаривание эпиморфизмов - тоже эпиморфизм.
По дуальности - получается, что мономорфизмы - тоже сохраняются при произведении или спаривании.
Но чего-то я пока туплю с диаграммами и ни одно из этих 4х утверждений не доказал.
Ну ок, если если в произведение хотя бы один мономорфизм, то и произведение - мономорфизм.
( http://planetmath.org/propertiesofmonomorphismsandepimorphisms )
Ну а с объединением мономорфизмов - всё сложнее...
Вроде Prop 4.2.6 в Handbook of Categorical Algebra -- что-то связанное с этим.
( https://books.google.ru/books?id=YfzImoopB-IC&pg=PA135&lpg=PA135&dq=finite+coproduct+of+monos&source=bl&ots=P_73eBmD3N&sig=Z2b0xVjInmMm1w_EFtfUf6IjOzY&hl=en&sa=X&ved=0ahUKEwiWhoXd-d_RAhXqFZoKHTthCJoQ6AEIJTAC#v=onepage&q=finite coproduct of monos&f=false )
Дан мономорфизм f:B>->1 (или эпиморфизм g:0->>B)
Верно ли утверждение, что "(B~0)\/(B~1)" где "~" - изоморфизм?
По определению моника, он обратим слева, т.е. i o f = Id_B, с другой же стороны f o i = Id_1 (потому что, по определению 1, из 1 в себя должен существовать ровно один морфизм). Что означает, что В и 1 изоморфны.
То, что ты говоришь верно для split monomorphism, то есть для секции, a я спрашиваю про обычный мономорфизм в произвольной категории.
Не надо применять "аксиому ковыбора", лол. :)
Slishkom tonko dlya menya. Всегда думал, что моник - это обратимый слева, на геометрическом языке - сечение, да. А как ещё?
А, извиняюсь, перепутал мономорфизм с коретракцией. Soryan.
В определении мономорфизма m нет квантора существования обратного слева к нему. m o f = m o g => f = g
Вот видишь, значит двач чему-то тебя научил.)
( Ответ на немного изменённый вопрос: )
Если g:0->>B эпиморфизм и B := 1, тогда получается, что, во-первых, 0 населён(internally inhabited),
во-вторых, получается категория, в которой глобальные элементы одного и того же множества - равны.
В такой категории выполняется "forall B,(B~0)\/(B~1)", если считать верным утверждение "во всякий B либо идёт морфизм из 1, либо не идёт".
Таким образом это зависит от разрешимости множества морфизмов из 1 в B.
 2,2 Мб, 3696x4928
2,2 Мб, 3696x4928Коединица, определённая через биекцию hom-множеств - не просто функция, переводящая одни объекты в другие, а аж натуральная трансформация функторов!
Всё записал на пикрелейтед(в обозначениях крупной статьи на вики, разумеется), но не вижу как доказать нижнюю коммутативную диаграмму, которая всё и докажет.
Откуда она следует?
S. Ramanan - Global Calculus
Juan A. Navarro Gonzalez - C^\infinity - Differentiable Spaces
Ещё на mathoverflow.net есть несколько обсуждений
>схемная идея
в смысле нильпотенты в структурном пучке?
бывает, почему. см.: комплексные пространства, в изводе Грауэрта
As David Mumford told me humorously, there was on the one hand the Zariski school in the United States, which had obtained many results using the method of resolution of singularities but which had already reached the limit.
“We were a group which had problems without methods, and on the other side Grothendieck had methods without problems.” So Zariski had the enormous generosity of sending all his students to learn Grothendieck’s ideas and the IHÉS became an annex of Harvard and Princeton. The second miracle consisted of a completely improbable collaboration between three very different people: Grothendieck, a prophet who was more interested in general ideas than in the details, Serre, an extremely logical spirit, precise, no nonsense, and Dieudonné, with his extraordinary capacity for work and understanding.
The Éléments and the Séminaires de Géométrie Algébrique are the result of this trio, on which no one would have bet.
>После добавления нильпотентных элементов к R получается лажа (типа R={0})
what?!
что за гнойная хуйня?
В принципе где топосы там ищи наебательство, но я совсем не понимаю, есть лекция шульмана, но я нифига не понял что там помимо нестандартного анализа.
Kock говорит что это по сути более удобное переложение идеи, которую придумал гротендик (the kth neigbourhood of the diagonal a.k.a. prolongation spaces of order k) а потом развили Malgrange, Kumpera и Spencer (есть даже книжка последних двух):
for the smooth case, Malgrange, Kumpera and Spencer, and others, described a category of “generalized differentiable manifolds with
nilpotent elements”
Smooth infinitesimal analysis — это просто добавление нильпотентов (в духе Гротендика) к алгебре функций, но для гладких многообразий.
Придумал это André Weil, его оригинальная статья по этой теме — «Théorie des points proches sur les variétés différentiables».
Да, я первокурсник. Спасибо, записал себе авторов на будущее.
Весь материал "Категорий для рабочего математика" умещается в первую главу Гельфанда-Манина (обоих книг).
Материал глав 6-9 у Вайбеля в Методах вообще отсутствует, а в 3 главе обзора представлен менее полно.
То есть о чем ты тут говоришь не ясно, но очевидно, что и сам этого не знаешь.
Спорно. Конусы и cocoon'усы у ГМ не рассматриваются так, как у Маклейна. Амальгамы, категория слайсов - где это всё?
http://dxdy.ru/topic115836.html
https://github.com/George66/Textbook
В определении через протоморфизмы ошибка.
Да, уже давно есть.
А мне нравится стрелочки рисовать.
Еще можно соконец, соднище, соторец (которец), соцель...
 57 Кб, 850x480
57 Кб, 850x480В чем принципиальная новизна и в чем отличие от общей алгебры?
Выглядит, как ребрендинг
Пойдёт. Лутьше, чем Маклейн, во всяком случае, хотя тоже не божья благодать. Посмотри вот эту https://arxiv.org/pdf/1612.09375v1.pdf
>>18526
Блядь, ну сколько ж можно. Про это уже столько написано и переписано, сломано копий, что в приличном обществе за такие похабные вопросы и по ебалу можно получить. Серьёзно, анончик, ну погугли что ли.
>>18545
Ну уверен, но вряд ли.
Бля, надо Бартошу сказать, а то он там целые курсы по теоркату в хаскеле ведет, а тут такие новости.
Ну беги скажи.
Это не новость, почитай Awodey.
http://lambda-the-ultimate.org/node/5435
Норм, "категории для гуманитариев"
Что это за интуиция такая, ничего не наоборот. Из XxY у тебя есть естественное отображение в X и в Y, а наоборот как?
Вот именно что дохуя. Для каждого элемента x из X у тебя есть своё отображение из Y в XxY: y |-> (x,y), для каждого y из Y есть отображение из X в XxY: x|->(x,y). Нет естественного выбора.
Ну тип доказательство лемм сводится к "водишь туда-сюда пальцем по диаграмме".
На libgen.io обычно покупаю.
 9 Кб, 597x556
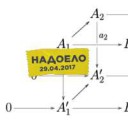
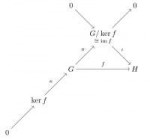
9 Кб, 597x556Почтенные мужи, в чём прикол ноликов на коммутативной диаграмме для первой теоремы о гомоморфизме групп?
Группа с одним элементом.
Так на языке точных последовательностей показывается инъективность и сюръективность.
Сказать что стрелка A->B инъективна (сюръективна) всё равно что сказать что последовательность 0->A->B (A->B->0) точна.
На bookfi.net
Для работающего математика не безумная.
я не он, но если в последовательности рисуются нули, то наверно предполагается, что она точная? А иначе зачем их рисовать?
Любой гомоморфизм f : A -> B даёт точную последовательность 0 -> ker f -> A -> im f -> 0.
Любая подгруппа A < B даёт точную последовательность 0 -> A -> B -> B/A -> 0. Это тоже легко проверить.
Ебать великая тайна раскрыта. Не то что хуесосы вроде Аводия бросающиеся "универсальностью", но блядь что это такое так нигде объяснения и нет.
Алсо, проиграл с упражнения. Можно так и в ебучку словить.
Похоже, неплохая книга.
я не знаю, что в алгебре может быть раньше слова "гомоморфизм". в принципе, ничего, это как бы часть определения основной категории, а раньше первого определения быть ничего не может
впрочем, я не знаю, о чём этот твой том ляйнстер. если он не про алгебру, то надо алгебры и навернуть, само собой
А по какой физике? Вообще там вроде из контекста можно как минимум найти, где узнать про гомоморфизм. Там ведь дохуя групп, векторных пространств и всего такого фигурирует по ходу. Вот там и пре-читай, например.
А вообще, как ни парадоксально, изучать котегории в общем без какого-то частного бэка тяжко по-моему. Не понимаешь, что это за такая поебень и зачем кому-то вообще этот огород нужно было городить. Вот когда ты гетнешь какой-то стек объектов, на которые натягиваются котегории, типа там те же множества, группы, топологические пространства, ты уже начинаешь понимать, что всё это нужно для определения функторов, а категории функторов, универсальность и вот это всё можно использовать для всякой весёлой поебени. Кстати, почему Лейнстер, а не Маклейн?
Хоть Аводий и не лучший вариант, но справедливости ради он поясняет за универсальность by example. В частности, прежде чем перейти к произведениям, он долго и нудно расписывает, что свободные моноиды на одном элементе изоморфны, аналогично и любые моноиды над данным множеством. Так что похоже проблема всё-таки в тебе, сорян.
Меня беспокоит именно само слово "универсальный". Это как если бы тебе привели тысячи примеров абелевых групп, но это вообще никак не поможет тебе додуматься до того что это блядь был такой математик и в честь него их так назвали.
Немного проблематично дать универсальное определение универсальности (pun intended). В простых терминах, это такое свойство объекта, которое делает все другие объекты, им обладающие, изоморфными данному. Но это определение на самом деле выглядит так себе. И Аводей приводит ненамного более внятное определение как "no junk, no noise". Оно хуёвое. Именно поэтому в данном случае определение через примеры лучше. Он писал, как умел. Не стреляйте в Аводея. Ну и опять повторюсь, я не его фанат. Лично мне Лейнстер нравится больше.
Не через граф, а через метаграф. Метаграфом называется не граф в привычном смысле, а формальная теория. Как формальная арифметика, например.
Так же, как и равенство двух отображений. Задай себе вопрос: когда два морфизма равны? Когда композиции двух морфизмов равны?
Реальная стори, я не тролль.
По сабжу только знаю что он еще более глобален чем теория множеств, а я как раз дрочу на такую абстракцию и generiлизацию. ну а еще хаскель ее юзает на котором я пишу хелловорлды, ясен хуй
Что ты несешь? Чистая теория множеств самая простейшая хуйня во всей математике, и именно хуйня потому что бесполезная. Какая глобальная? Её хватит описать одной двумя книгами, там и ничего нет практически.
Ладно, я имел ввиду не саму теорию множеств, а группы, поля и тд а они то определены на множествах!. Просто после школы охуел что все, что я изучал - поле с умножением и сложением над множеством действительных чисел ну и плюс несколько других операций, а что кроме этого есть еще бесконечное количество других полей, колец и другие более сложные струткуры, про которые я не знаю
Теорию множеств надо изучить, чтобы понимать это.
В школе не учат, как строятся действительные числа, а это между прочим реально существующий объект, как программа на компьютере. И десятичное представление чисел это не абстракция это реально ловишь все числа из этого множества, а не с какими-то яблоками, машинками работаешь, называя их количество. В этой книге The Real Numbers and Real Analysis (Ethan D. Bloch) первые 100 страниц посвящены этому, но там натуральные числа строятся как абстракция, в теории множеств конструктивно. Из этой книги узнаешь больше чем за 11 лет в школе.
Нет в хаскеле никаких категорий. Нет и не было, и не будет.
Линейная алгебра это основа современной математики. Потому если тебе не нравятся матрицы можешь забить вообще.
По книгам, не помню автора, но название "топосы, категорный анализ логики".
>а я как раз дрочу на такую абстракцию и generiлизацию.
ну и дурак
>ну а еще хаскель ее юзает на котором я пишу хелловорлды, ясен хуй
зачем тебе вообще математика?
а, ты же про теоркат спрашиваешь.
ну тогда хуй с тобой
Не знаю. Тут тысячи раз писали списки книг. Если знаешь английский возьми Акслера "linear algebra done right". Навряд ли лучше в виде учебника что-то есть.
А как же модули над кольцами? А Бурбаки? Зачем ты мальчику жизнь ломаешь?
Что ты не понимаешь?
>И там матриц нету??
Вроде как нет. Они и не нужны до того как ты не изучишь внешнюю алгебру.
Ну вот там пишут, комплексное число это упорядоченная пара {a, b}, я правильно понимаю что это сет из двух любых(определённым образом законтрейченных) элементов a и b который и есть комплексное число?
В фигурных скобках пишут множества. {a,b} это множество, содержащие a и b, а не упорядоченная пара. Пары обозначаются (a,b). Упорядоченная значит, что (a,b) != (b,a).
> {a,b} это множество содержащие a и b
то есть там может быть ещё много чего кроме a и b? то есть
1,3,7,a,8,b,4 и так бесконечно?
Нет там должно быть такое только {{...}, {...}}
Но вместо многоточия хоть бесконечно много чего, главное чтобы закрывались фигурными скобками с двух сторон.
То есть, я правильно понял, что когда мы делаем так {} то чтобы не оказалось внутри скобок это часть бесконечного набора?
Но ведь если мы делаем так {1, 2, 4} то мы так задаём набор ровно из трёх элементов? А так {1, 2, a} из бесконечного числа элементов так как есть буква?
>это часть бесконечного набора?
Нет. У тебя в наборе есть всё ровно то, что у тебя в скобках и ничего более. Некоторые наборы перечислить нельзя. Например множество всех точек окружности ты не перечислишь в скобках, но ты можешь сказать, что A именно такое множество.
>{1, 2, 4} то мы так задаём набор ровно из трёх элементов? А так {1, 2, a} из бесконечного числа элементов так как есть буква?
В обоих случаях 3 элемента.
Дополню, что {1,2,2}={1,2}, то есть и слева и справа всего 2 элемента.
Ну да у двоек же хеш одинаковый, лол
Хуйню ты написал, не будут так свойства упорядоченной пары выполняться. {a,{b}}
x = {c}
a = {{c}}
b = c
(a, b) = {a,{b}} = {{{c}},{c}} = {{x}, x} = (x, x), но x != a & x !=b
А должно быть так что (a, b) = (x, y) <=> a=x & b=y
Также хочется заметить, что логарифмирование секвераторных констант прямо пропорционально логарифмированию вариативных производных косинусов чисел, следовательно, степени и индексы можно спокойно упускать из тождеств.
The next talk will be livestreamed this week Thursday, 12 noon EST.
I'm going to speak about partial evaluations, the work that we did with the ACT School last year.
Email me if you want the access link, everyone is welcome.
Paolo Perrone
Strong Python programming skills, knowledge of NLP and ML are required, and category theory is a major bonus!
Here’s the job:
https://jobs.eu.lever.co/cambridgequantum/06744371-0e90-4d95-9007-d326504e381b
Слава тараканам
лучший вариант - изучать нормальную математику, теоркат придёт сам собой (в объёме, зависящем от твоей области)
>попытка формализации самого математического мышления?
я в таких категориях не мыслю, как по мне, это словоблудие
очень, правда, любимое многими анонами на доске
для меня теория категорий это просто удобный инструмент, чтобы организовывать взаимосвязи и упрощать язык, как-то так
вот этого матемачую. Это как изучать теорию множеств, может и содержательно, но наивного подхода и знания определений хватит в большей части математики.
Ну, теория категорий - это вполне самостоятельная наука. Не хуже и не лучше теории каких-нибудь других структур. Можно закопаться и что-то открыть.
1. Лившиц, Цаленко, Шульгейфер. Теория категорий. http://mi.mathnet.ru/inta5
2. Цаленко, Шульгейфер. Категории. http://mi.mathnet.ru/inta40
3. Цаленко, Шульгейфер. Категории. http://mi.mathnet.ru/inta71
Три обзора, сделанных с интервалом в несколько лет, первый в 1962 году, второй в 1969, третий в 1974. Интересны не только собственно текстом, но и прямо-таки здоровенной библиографией, частично до сих пор не потерявшей актуальность. Для полноты ссылок, наверное, стоит ещё упомянуть публикацию Шульгейфера с участием Куроша 1960 года, http://mi.mathnet.ru/umn6781
Скорее так
Этот обзор цаленко-шульгейферный входит в сборник "Общая алгебра" под ред. Скорнякова, более свежего образца.
Один раз пробовал через всем известную книгу, но там почти всюду упоминались структуры и связи между ними, ранее мне незнакомые.
А зачем входить в теоркат, если нет в голове структур, к которым его можно применить?
Ну когда пытался, мне очень понравилось рисовать стрелки и искать морфизмы из SET в RING, например. Но проблема в том что с кольцами не работал, а единственная алгебраическая структура, в которой я +- норм это магмы.
мне показалось, что удобнее всего входить через более-менее современные учебники по нужными тебе предметам, использующим теоркат как инструментарий: функан, алгебраическая геометрия, алгтоп, ...
там обычно в первых главах рассказываю быстренько все, что тебе надо + тебе интересно это читать, т.к. понятно, зачем ты это делаешь.
есть еще такая Category theory in context, но мне почему-то тяжеловато пошла - показалось, что плотность информации для моего слабого мозга великовата, хотя, конечно, проще маклейна
а в каком месте функану нужна теория категорий?
>Category theory in context
Эту книжку написала Emily Riehl
на тифаретники говорят, тётка очень зашкваренная (в том числе и в научном плане, вроде бы)
Может быть в современных конкретных работах и ни в каком, я, к сожалению, в функане не шарю. А тут я просто намекнул на книжку Хелемского по функану - не самое плохое введение в категории на конкретном примере.
а что с ней не так? просто функан скучный и сложный, а эта книжка - достаточно увлекательная. Что еще нужно для тех, кто не хочет специализироваться в функане надо?
весь алгебраический современный функан категорный погугли что такое КК-теория Каспарова, и что такое циклические гомологии алгебр Фреше, можешь ещё погуглить operator spaces, где базовая идея в том, что категорию банаховых алгебр хитрым образом твикают чтобы она стала более алгебраичной и более адекватно себя вести.
ну нет. Эта книга достаточно скучная, Саймон-Рид в десять раз интереснее. Если "специализировать в функане", то, возможно, да, но это само по себе звучит уныло.
Функан топ, лучше функана не бывает ничего
так-то напомню, что мы в треде про категории, а я в саймон-риде стрелочек не припомню
любой оператор есть стрелочка, так что не расстраивайтся
а так, небольшой оффтопик (полу)мёртвому треду никогда не помешает
стрелочки без коммутативных диаграмм - это еще не категории.
только диаграммный поиск, только хардкор!
глупости же
известная теорема устанавливает эквивалентность между абелевыми категорями и категорией модулей. это нивелирует необходимость в диаграммном поиске в абелевых категориях, а в других он и до того не был нужен
у вас бред. это никак не связано с абелевостью. chasing был есть и будед, алилуйя. любое доказательство сводится к поиску путей в графе.
любое пусть и сводится, если очень хочется, только никто так никогда не делает
да, там мерзкая и очень обидная какая-то была история
я не помню уже подробностей, но дорогой моему сердцу питер фрейд безусловно не в чём не виновен
Что он заабузил свою лоли-дочь?
> и категорией модулей
истинно так. сегодня вечером я очнулся и узрел, что все в мире состоит из модулей. даже категории! даже Гротендик!
Расширение модулей переломлено пополам
А наш батюшка Арнольд совсем усох
Он разложился на прямые слагаемые и на пересечение неприводимых подмодулей
А надстройка все идет и идет по конусу
И всё многообразие вложилось в $\mathbb{R}^N$
И весь мир состоит из модулей!
Модули над кольцом!
А моя судьба захотела на покой
Я обещал ей не участвовать в гомотопическом хаосе
Но на фуражке на моей коммутативная диаграмма и копредел
Как это трогательно коммутативная диаграмма и копредел
Лихая петля порождает фундаментальную группу
И весь мир состоит из модулей!
Модули над кольцом!
А моей статьёй накормили толпу
Анонимный рецензент нашёл в ней ошибку
Научное сообщество растоптало её на конференции
Так исправляйте же её сами
Потому что весь мир состоит из модулей!
Модули над кольцом!
Один лишь дедушка Шурик хороший был вождь
А все другие остальные такое дерьмо
А все другие враги и такие дураки
Над родною над математикой снег невежества шел
Я купил журнал LJ.ROSSIA там тоже хорошо
Там товарищ Миша там тоже что у нас
Я уверен, что у них то же самое
Весь мир состоит из модулей!
Модули над кольцом!
А при унивалентных основаниях все будет заебись
Их закончат скоро надо только подождать
Там все будет автоматически, там все будет в кайф
Там наверное вообще не надо будет ничего доказывать!
Я проснулся среди ночи и понял, что...
ПУЧОК МОДУЛЕЙ НАД ПУЧКОМ КОЛЕЦ
ПУЧОК МОДУЛЕЙ НАД ПУЧКОМ КОЛЕЦ
ПУЧОК МОДУЛЕЙ НАД ПУЧКОМ КОЛЕЦ
Расширение модулей переломлено пополам
А наш батюшка Арнольд совсем усох
Он разложился на прямые слагаемые и на пересечение неприводимых подмодулей
А надстройка все идет и идет по конусу
И всё многообразие вложилось в $\mathbb{R}^N$
И весь мир состоит из модулей!
Модули над кольцом!
А моя судьба захотела на покой
Я обещал ей не участвовать в гомотопическом хаосе
Но на фуражке на моей коммутативная диаграмма и копредел
Как это трогательно коммутативная диаграмма и копредел
Лихая петля порождает фундаментальную группу
И весь мир состоит из модулей!
Модули над кольцом!
А моей статьёй накормили толпу
Анонимный рецензент нашёл в ней ошибку
Научное сообщество растоптало её на конференции
Так исправляйте же её сами
Потому что весь мир состоит из модулей!
Модули над кольцом!
Один лишь дедушка Шурик хороший был вождь
А все другие остальные такое дерьмо
А все другие враги и такие дураки
Над родною над математикой снег невежества шел
Я купил журнал LJ.ROSSIA там тоже хорошо
Там товарищ Миша там тоже что у нас
Я уверен, что у них то же самое
Весь мир состоит из модулей!
Модули над кольцом!
А при унивалентных основаниях все будет заебись
Их закончат скоро надо только подождать
Там все будет автоматически, там все будет в кайф
Там наверное вообще не надо будет ничего доказывать!
Я проснулся среди ночи и понял, что...
ПУЧОК МОДУЛЕЙ НАД ПУЧКОМ КОЛЕЦ
ПУЧОК МОДУЛЕЙ НАД ПУЧКОМ КОЛЕЦ
ПУЧОК МОДУЛЕЙ НАД ПУЧКОМ КОЛЕЦ
все правильно анон написал, вот только
>при унивалентных основаниях все будет
сильно пахнет счастливым будущим коммунизма
Где раздобыть эту школьную программу по мотивам Бурбаков?
С какой книги нАчять?
Определение 1. Категория категорий (кк) - такая категория, что каждый её объект - категория; каждый морфизм - функтор между соответствующими категориями, тождественный морфизм - функтор id, композиция морфизмов - композиция функторов.
Универсальная категория Un - такая кк, что любая категория изоморфна какому-то объекту из Un. Докажем, что универсальной кк не бывает.
Рассмотрим, согласно Маклейну, категории под названием 2 и 3 - соответственно стрелку между двумя точками и коммутативный треугольник. Будем говорить, что некоторая кк содержит 2 и 3, если она содержит объекты, изоморфные 2 и 3.
Лемма 1. Пусть A и B - две изоморфные кк, и пусть 2 и 3 являются объектами A. Тогда объекты A изоморфны объектам B, и наоборот, объекты B изоморфны объектам A.
В самом деле, пусть С - некоторая категория, являющаяся объектом A. Тогда каждый морфизм C соответствует функтору из 2 в C. Иными словами, класс морфизмов категории C биективно соответствует классу Hom(2,C) - классу стрелок из объекта 2 в объект C в категории A. Далее, закон композиции морфизмов в C задан, если задан набор всех возможных коммутативных треугольников в C. Набор коммутативных треугольников в C полностью определяется функторами из 3 в C - то есть полностью определяется классом Hom(3,C) категории A.
Таким образом, для любого объекта x категории A структура категории на x полностью определяется классами Hom(2,x) и Hom(3,x). Категории A и B изоморфны по условию, значит, hom'ы у них одинаковые. Отсюда следует лемма.
Определение 2. Категория категорий называется расселовской, если она изоморфна некоторому своему объекту.
Лемма 2. Пусть 2 и 3 являются объектами категории A, и A изоморфна какой-то расселовской категории B. Тогда и сама A является расселовской.
Доказательство. В категории B есть объект x, изоморфный B. По лемме 1, каждый объект B изоморфен некоторому объекту категории A. Значит, в A есть объект x', изоморфный B. Поскольку B изоморфна A, получаем, что x' изоморфен A. Значит, A изоморфна своему объекту.
Теперь, собственно, доказательство несуществования Un.
Пусть R - категория, объектами которой являются те и только те объекты Un, которые не изоморфны расселовским категориям (а стрелки - всевозможные функторы). Un, в силу универсальности, имеет объект R', изоморфный R.
Un содержит 2 и 3 - она же универсальная. 2 и 3 не расселовские, поэтому R содержит 2 и 3. Если R расселовская, то содержит объект x, изоморфный R, вопреки определению R (получается, что x изоморфен расселовской категории). Значит, R не расселовская. Поэтому лемма 2 запрещает R быть изоморфной какой-то расселовской категории. Значит, R' тоже не расселовская и поэтому является элементом R. Значит, R расселовская. Получили, что оба варианта дают противоречие.
Из https://arhivach.net/thread/683743/
Уточнение: категории категорий считаются полными, то есть hom(c,d) - класс всех функторов из c в d.
Определение 1. Категория категорий (кк) - такая категория, что каждый её объект - категория; каждый морфизм - функтор между соответствующими категориями, тождественный морфизм - функтор id, композиция морфизмов - композиция функторов.
Универсальная категория Un - такая кк, что любая категория изоморфна какому-то объекту из Un. Докажем, что универсальной кк не бывает.
Рассмотрим, согласно Маклейну, категории под названием 2 и 3 - соответственно стрелку между двумя точками и коммутативный треугольник. Будем говорить, что некоторая кк содержит 2 и 3, если она содержит объекты, изоморфные 2 и 3.
Лемма 1. Пусть A и B - две изоморфные кк, и пусть 2 и 3 являются объектами A. Тогда объекты A изоморфны объектам B, и наоборот, объекты B изоморфны объектам A.
В самом деле, пусть С - некоторая категория, являющаяся объектом A. Тогда каждый морфизм C соответствует функтору из 2 в C. Иными словами, класс морфизмов категории C биективно соответствует классу Hom(2,C) - классу стрелок из объекта 2 в объект C в категории A. Далее, закон композиции морфизмов в C задан, если задан набор всех возможных коммутативных треугольников в C. Набор коммутативных треугольников в C полностью определяется функторами из 3 в C - то есть полностью определяется классом Hom(3,C) категории A.
Таким образом, для любого объекта x категории A структура категории на x полностью определяется классами Hom(2,x) и Hom(3,x). Категории A и B изоморфны по условию, значит, hom'ы у них одинаковые. Отсюда следует лемма.
Определение 2. Категория категорий называется расселовской, если она изоморфна некоторому своему объекту.
Лемма 2. Пусть 2 и 3 являются объектами категории A, и A изоморфна какой-то расселовской категории B. Тогда и сама A является расселовской.
Доказательство. В категории B есть объект x, изоморфный B. По лемме 1, каждый объект B изоморфен некоторому объекту категории A. Значит, в A есть объект x', изоморфный B. Поскольку B изоморфна A, получаем, что x' изоморфен A. Значит, A изоморфна своему объекту.
Теперь, собственно, доказательство несуществования Un.
Пусть R - категория, объектами которой являются те и только те объекты Un, которые не изоморфны расселовским категориям (а стрелки - всевозможные функторы). Un, в силу универсальности, имеет объект R', изоморфный R.
Un содержит 2 и 3 - она же универсальная. 2 и 3 не расселовские, поэтому R содержит 2 и 3. Если R расселовская, то содержит объект x, изоморфный R, вопреки определению R (получается, что x изоморфен расселовской категории). Значит, R не расселовская. Поэтому лемма 2 запрещает R быть изоморфной какой-то расселовской категории. Значит, R' тоже не расселовская и поэтому является элементом R. Значит, R расселовская. Получили, что оба варианта дают противоречие.
Из https://arhivach.net/thread/683743/
Уточнение: категории категорий считаются полными, то есть hom(c,d) - класс всех функторов из c в d.
Со столь неконкретными претензиями, пожалуйста, проследуйте в какой-нибудь троллотред.
вижу, в первый раз не дочитал твоё доказательство
вижу, ты упираешь на парадокс рассела, детали мне читать не хочется. насколько я могу судить, доказательство, если оно верное, должно упираться как-то в различия между "класс" и "множество"
Нет, отнюдь. Доказательство остаётся валидным для любой подлежащей теории множеств, если в ней есть схема выделения подмножеств. Категория всех категорий невозможна не из-за того, что она слишком большая, а по соображениям самореференции.
короче, ты парадокс лжеца поместил в простыню текста. ну ладно, пускай
помнится, меня учили, если не разрешать множествам быть слишком большими, "самореференции" не получаются (или даже запрещаются прямо, я уж не вспомню). например, если всё положить в один универсум Гротендика, тоже разве не получится?
впрочем, ответ на вопрос меня мало волнует, если честно
Если фиксирован универсум, то категория всех малых категорий относительно этого универсума существует. Сама она, понятно, малой не является.
>ты парадокс лжеца поместил в простыню текста
Главная техническая деталь - что в категории категорий hom(2,C) и hom(3,C) полностью определяют структуру категории в C.
ну типа там можно такие коммутативные диаграммы рисовать мне неохота пояснять детали
Вообще-то, если текст хороший, там ниже должно поясняться исключение: текст не для начинающих изучать теоркат, правда, непонятно тогда, зачем формулировать лемму ионеды
В общей ситуации, если у тебя есть два функтора $F,G$ и для каждого объекта $A$ задана стрелочка $\varphi\colon F(A) \to G(A)$, то для любого морфизма $A \to A'$ можно рисовать диаграмму, в которой на горизонталях стоят $\varphi\colon F(A) \to G(A)$ и $\varphi\colon F(A') \to G(A')$, а на вертикалях - значения функторов $F,G$ на морфизме морфизме $A \to A'$. Говорят, что стрелочка $\varphi$ естественна по $A$, если всякая такая диаграмма коммутативна. На более формальном языке это означает, что $\varphi$ образует морфизм функторов $F \to G$ (естественное преобразование, отсюда и терминология). Если при этом, скажем, добавлено, что $\varphi\colon F(A) \to G(A)$ есть изоморфизм для всех $A$, то $\varphi$ доставляет изоморфизм функторов.
насчёт деталей, относящихся к лемме Йонеда, это, грешен, я уже не в силах
(меня и на основное её утверждение никогда уже не хватало)
Спасибо, но это немного не то. Определение естественного преобразования понятное. Вопрос же был о том, что такое естественность "по объекту c и по функтору F".
именно то
У тебя там изоморфизм между двумя хренями, которые зависят от c и F. Эти хрени надо вообразить себе как функторы (как они действуют на морфизмы между объектами типа c и F) и рисовать диаграммы, как я указал. Естественность означает коммутативность этих диаграмм
Сап, категорщики! Как вкатиться в эту область с нуля? В матане не шарю, посоветуйте с чего начать?
Эти картинки можно переформулировать в терминах теории множеств.
Любое утверждение о множествах можно переформулировать в терминах теории групп или в терминах графов.
Сформулируй "если есть инъекция из А в В и из В в А, то А и В равномощны" в терминах теории групп
Бамп вопросу.
 51 Кб, 215x211
51 Кб, 215x211посмеялся с картинки
Спектральные последовательности для когомологий пучков ничем не отличаются от других спектральных последовательностей, поскольку в сущности это все равно все в абелевой категории делается, а состоит она из пучков или из модулей, уже не суть важно
спасибо, я это понимаю. Просто мне кажется, что существуют источники где более подробно говорится о спектралках для пучков, типа Бейлинсона; про которые я собственно и спрашивал
Да, понятна. Вопрос был конкретно о том, как выглядит диаграмма для этого жаргонного выражения. Если бы это был вопрос о моноиде, то нужна была бы вот эта картинка.
ну ок
Не, тут не то что мне нужно, мне нужно для variety а тут какие-то manifodы и вообще чето не то всё это
про линейные пространства можно думать очень просто:
изоморфизм между $V$ и $V^*$ в отсутствии скалярного произведения нельзя придумать никаким образом, не привлекая дополнительных построений, а если их привлекать, то изоморфизм построить можно, но будет от них зависеть (например, можно его построить выбрав базис, но тогда будет зависеть от базиса)
в то же время, если на $V$ введена дополнительная структура "скалярное произведение", то мы можем написать изоморфизм, который эту структуру использует. однако теперь она к $V$ привязана и никак уже не выбирается; поскольку она зафиксирована, мы говорим, что он ни от каких дополнительных построений наш изоморфизм теперь не зависит (только от заданных уже структур), тем он естественный
точное определение в смысле теории категорий я пояснял выше по треду: >>84021
коротко говоря, "естественный изоморфизм" - это изоморфизм функторов
>>85010
имеем $h \circ f = g \circ f = \operatorname{id}_A$ и
$f \circ h = f \circ g = \operatorname{id}_B$
эти соотношения означают, что оба морфизма $g,h$ суть двусторонние обратные к $f$, следовательно, они равны; это противоречит условию (что они разные)
Господи, спасибо тебе, спасибо, анон. Очень понравилось обьяснение через
>не привлекая дополнительных построений
Мимо другой, но можно ли найти объяснение на пальцах почему ломается изоморфизм между векторным пространством и дважды сопряженным, в случае бесконечной размерности.
потому что каноническое отображение $V \to V^{\ast\ast}$ является мономорфизмом, при этом (в конечномерном случае) $\dim V = \dim V^{\ast\ast}$. В бесконечномерном размерностей конечных нету, и начинаются патологии: одной мономорфности, чтобы был изоморфизм, уже недостаточно
Вообще, конечномерные векторные пространства похожи на конечные множества: с конечными множествами всё хорошо, а в бесконечности начинается всякое; из счётного множества (скажем, базиса в бесконечномерном пространстве) можно вытащить два непересекающихся равномощных с ним, например.
зачем? берёшь в натуральных чётные и нечётные числа, и всё
 118 Кб, 1280x720
118 Кб, 1280x720Category Theory for Computing Science Michael Barr Charles Wells норм тема?
Олсо что такое "basic language of mathematics and computing science of the sort taught in an introductory discrete mathematics course"? Что в него должно входить?
Я знаю что есть там всякие множества, ряды, графы, матрицы, ещё какая-то хуйня. Что такое изоморфизмы и группы не знаю.
>Что в него должно входить?
Там есть глава Preliminaries, почитай её. Если можешь эту главу осилить - читай дальше. Так можешь и с книгами по другим темам поступать, кстати - если начало идёт тяжко, сходи подкачайся.
>норм тема?
От книги тут ничего не зависит. Ты собрался читать теорию или скорее язык, разработанный математиками для математиков на основе десятилетий математических задач и примеров из нескольких огромных математических разделов. Если тебя это не смущает, то читай любую вводную книгу, они все одинаковые.
Теоркат в CS - это решение в поисках задачи. На выходе - китайская комната с сотней определений и двумя искуственными примерами. Как это взлетело, до сих пор не понимаю. Смысл говорить про естественные преобразования или даже функторы, если у тебя там 1.5 категории всего.
> Теоркат в CS - это решение в поисках задачи. На выходе - китайская комната с сотней определений и двумя искуственными примерами. Как это взлетело, до сих пор не понимаю. Смысл говорить про естественные преобразования или даже функторы, если у тебя там 1.5 категории всего.
Ну, вообще согл++. Тупа модно стильно молодёжно.
>Теоркат в CS - это решение в поисках задачи. На выходе - китайская комната с сотней определений и двумя искуственными примерами. Как это взлетело, до сих пор не понимаю. Смысл говорить про естественные преобразования или даже функторы, если у тебя там 1.5 категории всего.
Ну понятно, что если не лезть в чисто теоретические части CS с категорными моделями теорий типов, то там действительно все примерно на уровне того, чтобы говорить о монаде действующей на одной данной категории. С другой стороны, сами обобщения такого рода видимо вполне удобны для программистов (если бы они не знали о категориях, то наверное все-равно что-то функционально похожее придумали бы).
 95 Кб, 672x287
95 Кб, 672x287Вот у меня есть какой-то текст на человеческом языке.
Текст это очевидно моноид, потому что к любому предложению можно добавить следующее.
(Текст может быть в виде юникод-строки например но это не важно)
Пусть этот моноид будет Z
Далее у меня есть какой-то способ закодировать произвольный текст словарем V фиксированной длины
То есть получается морфизм V -> Z
При этом образ всего V может не совпадать с Z
Если я еще хочу чтобы совпадал, то как это называется?
И если я возьму все подобные кодировки V*->Z , какая структура получается, и что про нее интересного науке известно?
 143 Кб, 1555x452
143 Кб, 1555x452С ними имел дело в алегеме. Я хочу именно интересные вещи в категориях.
1. Самую базу. И теорию типов на уровне книжки про гомотопическую теорию типов.
2. Хочу изучить их применение к философии и логике, заметил некоторые интересные вещи (помимо интерпретации в духе диалектического кринжа). Нужно изучать теорию топосов?
>Хочу изучить их применение к философии и логике
Есть стандартные работы по приложениям к логике, и для них как правило нужны топосы, да. Вот тут наверное самый полный список (вводной) литературы по теме, который можно найти: https://plato.stanford.edu/Entries/category-theory/bib.html
Еще советую посмотреть сюда https://awodey.github.io/catlog/ и сюда https://diliberti.github.io/Teaching/Teaching.html
Начинать имеет смысл с книжки Голдблатта. На русском еще есть книжка Васюкова "Категорная логика", которая про приложения к неклассическим логикам (на английском монографий по этой теме, насколько я знаю, нет), но педагогически она, по-моему, отвратительна, и научиться из нее чему-то сложно.
Во, кстати, все говорят про Маклейна и категории для работающего, но ведь книжка Аводи - топчик. И для начинающего прям самое оно. Правда, там были неточности. Но это в мои времена, 13й-14й года, когда я её проштудировал
>Во, кстати, все говорят про Маклейна и категории для работающего, но ведь книжка Аводи - топчик
Это какая? "Introduction to Categorical Logic"? Так наверное потому и не говорят, что в ней математики в принципе и нет. И поэтому и говорят про книжку Маклейна, который собственно сам предмет и придумал, и который написал эту книжку для таких же математиков, как он сам, а не для "математиков" типа Аводи, которые суть погромисты, ларпающие математиков, и больше времени проводят на гитхабе.
Посмотрел, сорта говна. Никакой математики, никаких примеров из модулей\алгтопа\алгема, просто сухой теоркат, таких книг десятки. Где-то там в задачках что-то изолированное промелькивает про группы и топологии, и всё. Поэтому для математиков это всё равно хуита.
Маклейн крутился в среде Вейля и Нётер, а Аводи крутился в среде Маклейна. Если составить точную последовательность, то Аводи как раз и будет теоркатом, профакторенным по содержательной математике.
ну давай, пучкни, хочешь же
А ты эту книгу вообще открывал, чмошник?
ниасилятор, короче.
> пержу про пучки
> не вижу их в упор
Хули с тебя взять, ниасилятор. Решение задачек из учебников с помощью жпт - твой верх.
>Маклейн крутился в среде Вейля и Нётер, а Аводи крутился в среде Маклейна. Если составить точную последовательность, то Аводи как раз и будет теоркатом, профакторенным по содержательной математике.
слишком сложная для местных основателей аналогия
в математических статьях тоже рассматриваешь точки и запятые вместо чтения? сразу видно бездарного любителя засунуть себе логику поглубже в очко
Уёбище, не способное родной язык выучить, не в состоянии освоить язык математики, таракаш.
по тебе и видно, кек
обычно математики (русскоязычные) пишут довольно грамотно (на русском). ну, а в журналах уже редактура есть. понятно, однако, что придирки до размера печатных букв в интернетах едва ли имеют какое-то отношение к вопросам грамотности. это давно стало (в интернетах по сути и всегда было) больше элементом стиля, чем указанием на неспособность автора питать грамотно. тем самым, придираться к "мелкобуквам" и делать из этого выводы может позволить себе только тупой вонючий мудила, которому доебаться больше не до чего. ясно, что подобное говно либо посылать нахуй и игнорировать, либо сразу игнорировать, а большего внимания оно не заслуживает
kaledin vobshe pishet vot tak na tifarete. emu len raskladku perekluchat
Хули, это прощем, чем статьи писать.
Ты с несколькими анонами общаешься, мудило напыщенное.
>доказываем теоремы с помощью diagram chasing
И как именно вы это делаете, как удобнее всего? Не через Фройда-Митчелла же, иначе не дидов гнать не стали бы.
Содержательная теория категорий проходится после общей алгебры и/или основ теории гомотопий.
А так просто чтобы уметь символами крутить, то достаточно знакомства с понятием функции.