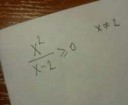Это копия, сохраненная 6 января 2017 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.

1. Берешь какой-то список попонтовее. Не дай бог прочитать книгу, которой там нет, рисково это, можно зашквариться.
2. Заучиваешь наизусть определения. Не пытайся обдумывать прочитанное, это занимает слишком много времени, а тебе нужно успеть дойти до настоящей современной математики.
3. Раз в неделю заходи на архив, выбирай рандомную статью и несколько секунд читай несколько первых строк. Особый шик — запомнить название. Так ты приобщаешься к современным исследованиям. На забудь скачать статьи Мочидзуки.
4. Ежедневно посещай блог вербита и математические треды. Глубокие обсуждения математических проблем в среде настоящих специалистов помогут повысить уровень математической культуры для недосягаемых академическому быдлу высот.
5. Настоящая математика только на английском. Постепенно прекращай читать книги, написанные по-русски, да и вобще любые, зато показывай всем, как ты знаешь английский, а не то примут за картофана.
6. Интегралы, которые тебе задают на первом курсе, решать не обязательно, это называется вторая культура.
7. Ну и что, что тебя выперли из вузика? Это и вузом то назвать было нельзя, так, картофельная плантация, работники которой реконструируют математику допотопных времен. Вон, вербита тоже выперли. Настоящее образование только за границей. Злая судьба забросила тебя в водочный ад, но рано или поздно, благодаря своему упорному труду ты выберешься в Гарвард, где будешь раз в неделю ходить на семинары по теарам Ходжа по выбору.
8. К этому моменту можно самому составлять списки, давать советы, отвечать на вопросы. Списки составляются очень легко: берешь готовый от вербита и меняшь местами названия. Можно взять парочку и перемешать.
9. Отвечать на вопросы тоже очень просто: если увидел знакомые слова — перепечатывай соответствующие определения из книги. Если незнакомые — это картофан, гони его ссаными тряпками.
В точности следуя этим советам ты станешь Настоящим Первокультурым Математиком и сможешь посвящать свободное от жалоб мамки время на улучшение научной атмосферы в парашке путем остроумных дискуссий в сети
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
42. https://arhivach.org/thread/145879/
43. https://arhivach.org/thread/146833/
44. https://arhivach.org/thread/152600/
45. https://arhivach.org/thread/153157/
46. https://arhivach.org/thread/156244/
47. https://arhivach.org/thread/159628/
48. https://arhivach.org/thread/165872/
49. https://arhivach.org/thread/183576/
50. https://arhivach.org/thread/187447/
51. https://arhivach.org/thread/188358/
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
42. https://arhivach.org/thread/145879/
43. https://arhivach.org/thread/146833/
44. https://arhivach.org/thread/152600/
45. https://arhivach.org/thread/153157/
46. https://arhivach.org/thread/156244/
47. https://arhivach.org/thread/159628/
48. https://arhivach.org/thread/165872/
49. https://arhivach.org/thread/183576/
50. https://arhivach.org/thread/187447/
51. https://arhivach.org/thread/188358/
Поясните за первый ОП-пик. В чем смысл?
Сам не знаю. Наверное, школьница, рисовавшая это, так воспринимает производную.
Кстати, пикчи - рандом.
Оп, иди в пизду со своим Гарвардом. Таких как ты пиздаболов надо уничтожать. Не удивлюсь, если Обама дальний твой родственник или близкий . Нормальная подача материала в детстве и любовь, залог успешного математика. Я бы уже книгу давно написал, на которую дрочили бы все энштейны. А сколько бы законов открыл... Пиздуй в Гарвард на фуршет и улыбайся седым профессорам.
Проигрывал, как ебанутый, хоть и тупо это всё. Только в последнем не понятно, какая логика у философа.
Проигрывал, как ебанутый, хоть и тупо это всё. Только в последнем не понятно, какая логика у философа.
Философская. That's the point.
Ну поговорил. Тем более минус этой доске, где блять пасты дублируют, наукач неебаться. Постоянным посетителям привет!

В треде для начинающих все спят. Спрашиваю здесь.
ПАМАГИТИ ПОНЯТЬ ГАУССА БОННЕ
в случае многообразия с краем.
Доложите мне всё, что вы про него знаете
3 раза перечитал ОП-пост, но так и не смог понять, это сарказм или нет?
Я надеюсь, что твой пост это сарказм.
Боны какие-то, ты что нацист? Может еще гитлера уважаешь?

У меня вопросы по приведению матрицы к ступенчатому виду.
Есть 5 элементарных преобразований. Но как понять, какое ИМЕННО преобразование нужно в данной ситуации?
Например, в матрице на пиктрилейтед можно как поменять местами 1 и 4 столбцы, так и вычесть из 1-й строки умноженную на 2 2-ую. И так далее.
Может, элементы матрицы при одной последовательности преобразований не будут равны элементам при другой (кстати, они будут?). Но при этом ранг и определитель не изменятся, верно?
Если ты делаешь это приведение для решения систем-столбцы лучше не трогать. Берёшь вторую строку, отнимаешь домноженную на коэффициент первую, получаешь ноль, повторяешь с остальными строками, получаешь в первом столбце нули везде, кроме первой строки. Далее то же с отниманием второй строки у следующих. Это не единственный способ конечно, просто так проще.
Ранг от таких преобразований не меняется вообще.
Мог бы придумать и написать. Кто же тебя будет проверять.
С карточными стратегиями успех может быть только вида "написал книгу о том как с помощью матёшки легко выиграть у казино и впарил лохам".
Есть же более менее надежный способ - после каждого проигрыша удваивать ставку.
А ну да, и это тоже. Но там тоже не так всё просто, короче, разбираться надо. Вот я разобрался, скоро книгу допишу, можете купить и тоже попробовать.
>Есть же более менее надежный способ - после каждого проигрыша удваивать ставку.
1. Деньги у тебя не безлимитные.
2. Специально для таких умных в казино обычно действует лимит на количество ставок.
3. Для самых упорных и старательных - игры в казино устроены таким образом, что вероятность выиграть не 50%, а чуть меньше. На рулетке шансы жрёт зеро, в хитромудые правила блекджека давно напиханы костыли. Таким образом, на длинных сериях мартингейлобляди сасают.
Исключение разве что покер, но казино с ним предпочитают не связываться, а немножко заработать на чемпионатах таки можно.
Sowa это Федор Богомолов.
Хуйня и под коня. Смотри: ты ставишь 1$, если выигрываешь - красавчик, если нет - ставишь 2$ и т.д. допустим, у тебя есть 1023$ - тогда ты можешь сделать 10 таких ставок подряд, если не будешь выигрывать. Если бы это была не рулетка, а просто подбрасывание монетки, то у тебя был бы 1023/1024 выиграть жалкий один доллар, а в оставшемся проиграть все 1023$. Матожидание выигрыша ноль. НО: в рулетке есть зеро и картина другая. С шансом чуть больше одной тысячной ты проигрываешь 1023$, во всех остальных выигрываешь один доллар и матожидание выигрыша отрицательное.. Ты оперируешь гигантскими суммами (которые невозможно получить ни мартингейлом, ни даламбером), а в качестве приза каждый раз получаешь жалкие гроши. Мартингейл сосёт, в общем.
P.S: в казино есть минимальная и максимальная ставка, например, от 10 до 200 баксов, специально для мартингейльщиокв.
P.P.S: более интересна игра с подбрасыванием монетки, в которой если на первый раз выпала решка, то ты получаешь 1$ и игра прекращается, если орёл - подбрасываем второй раз, и на нём есть шанс выиграть 2$, на третьем 4, на пятом 8 и т.д. игра продолжается до первой решки.
О. За Новороссию, в туза не долбится, порицаем вербитоблядями. Такого надо поддерживать!
Лекции, из которых первый отрывок, так и не досмотрел. Всё пытается охватить, потом начал теорию категорий рассказывать, хотя начал с гипотезы Римана, после которой остались непонятные куски знаний.
Он у мамки альфач, с профессией просто промахнулся
Не поделили, а умножилии и на том хорошо.
Спасибо.
откуда вторая?
я тоже хочу коалгебры поучить
у него этих лекций миллион на лекториуме, я не знаю, какой курс выбрать.
Алгебры Хопфа.
Курс "Алгебры Хопфа и теория Галуа" на лекториуме/ютубе

Тебе бан за перевод ника. Только red herring этого дида-пидора можно называть, никаких селедок.
>>381758
схуяли придумал эйнштейн. он же сам их побаивался по первости, тензоров етих.
а, торможу, обсуждали уже "тензоры имени эншейтна" здесь, большим бугуртом дело закончилось, а я забыл совсем.
Допустим мы вынимаем из колоды в 52 карты n карт. Какой шанс достать те же карты (в любом порядке) во второй раз? Ну, или, проще говоря, каков шанс достать определенную комбинацию карт, в любой последовательности?
Когда n = 1, это понятно, 1/52. Но когда n = 51 шанс тоже 1/52 (потому что карте оказаться первой или последней шансы одинаковые).
Из этого, вроде выходит, что достать 13 карт и достать 39 карт шансы одинаковые (потому что у нас в другой стопке остается 39 и 13 карт соотвественно и это просто frame of reference). Так, или я все ж где-то накосячил в рассуждениях?
Так или иначе, должна ж быть какая-то формула, куда можно подставить n получить вероятность, да?
Открой любой учебник по теорверу и почитай первые 10 страниц.
Ответ 52 x 51 x ... x (52 - n + 1).
>как вообще возможно сесть и описать какой-либо процесс?
Математическая модель же. Делаем более-менее обоснованные утверждения о характере прохождения процесса, пишем уравнения, решаем их
Я уточню. У меня есть 6 параметров с помощью которых можно описать определенный процесс. Про параметры известно только их граничные значения. Есть условия, например, можно сказать с уверенностью, что параметр x3 вносит больший вклад в возрастание процесса, x2 - скорее всего оказывает несильное влияние, а x1 - может как увеличивать скорость возрастания функции, так и уменьшать в зависимости от значения и т.д.
Необходимо написать уравнение, которое в соответствии с условиями было бы достаточным точным для описания этого абстрактного процесса.
Если вы знаете как сделать это, то подскажите, что гуглить, читать на решение подобной задачи. Спасибо.
Спасибо, почитаю про математические модели.
Список книг, заслуживших всенародное признание и любовь
В этом списке - книги, по которым мы учились и которые мы уважаем и ценим.
Эти учебники, по нашему общему мнению, существенно лучше многих других.
Звёздочкой отмечены книги, разыскиваемые в электронном виде. (Остальные уже
сосканированы.)
Рекомендации взяты из дискуссии, так что слово "я" это кто угодно.
Математика
Начальное изучение
"Числа и фигуры" Радемахера и Теплица
"Наглядная геометрия" Гильберта и Кон-Фоссена
"Что такое математика" Куранта и Роббинса
"Арифметика" Серра
Высшая математика
Мат. анализ, дифф. уравнения?
Рудин. Курс мат. анализа
Гурса, Кудрявцев, Никольский - разные курсы мат. анализа
Смирнов. Курс высшей математики
Петровский. Курс дифференциальных уравнений
Демидович. Задачник по мат. анализу
Филиппов. Задачник по дифф. уравнениям
А. Найфе "Методы возмущений". Необходимая книга после изучения мат.
анализа и дифф. уравнений, чтобы научиться считать асимптотики для точно нерешаемых задач.
ТФКП:
Ю.В.Сидоров, Федорюк, М.И.Шабунин. Лекции по ТФКП. (начальный)
Лаврентьев, Шабат. Методы ТФКП (более продвинутый)
Линейная алгебра:
Гельфанд. Лекции по линейной алгебре
Беклемишев. Лекции по аналитической геометрии (но плохо про тензорную алгебру!)
Очень простая со множеством примеров книжка по тензорному анализу
как первый учебник -
А.И. Борисенко и И.Е. Тарапов. Векторный и тензорный анализ с приложениями
(переведена на англ. и на западе пользуется большой популярностью, регулярно
переиздается в изд. Dover)
Дифф. геометрия и топология:
Стинрод, Чинн. Первые понятия топологии (школьный уровень)
Александров, Евремович. Топология
По топологии на западе считается одним из самым хороших учебников это
James R. Munkres, Topology. (2nd Ed включает общую и алгебраическую топологию)
Ясный стиль, тщательно подобраны примеры, продуманная структура изложения...
Могу лично подтвердить - лучше этой пока ничего не видал.
Дубровин, Новиков, Фоменко. Современная геометрия (физикам-теоретикам - особенно полезно)
Шварц. Квантовая теория поля и топология (это на самом деле книга по
алгебраической топологии, а не по физике, но очень хорошая)
"Теория Морса" Милнора
Spivak, Michael. A Comprehensive Introduction to Differential Geometry,
2ndEd. Berkeley, CA: Publish or Perish 1999 5 томов
B. O'Neil Elementary Differential Geometry, 2ndEd. (из всех западных
самое толковая и простая трактовка диф.геомет с объяснением смысла)
Функциональный анализ:
Линейная алгебра (подготовка к функану)
Глазман И.М., Любич Ю.И. Конечномерный линейный анализ в задачах.- М.: Наука, 1969.- 476с.
супер задачник по функану:
Кириллов А. А., Гвишиани А.Д. Теоремы и задачи функционального анализа. Изд.
2-е, перераб. и доп.-М.: Наука, 1988.-396 с.
еще по функану хорош Колмогоров-Фомин, а как подготовка -
матанализ по Рудину.
Мат. физика:
Арфкен. Методы математической физики
Чистая математика
Гриффитс, Харрис. Алгебраическая геометрия
Прикладная математика, численные методы
Price, Teukolsky, et al. Numerical recipes (хорошие объяснения методов, но
плохие программы к ним, так что писать программы надо самим
- методы также частично устарели, но всё равно как
вводный курс непревзойдённо)
Теория информации
Классика (значит "читал сам, постоянные ссылки в литературе"):
Robert G. Gallager
Information Theory and Reliable Communication
Wiley Text Books; (1968), 608 pages, ISBN: 0471290483
Thomas M. Cover, Joy A. Thomas
Elements of Information Theory
Wiley-Interscience; (August 12, 1991), 542 pages, ISBN: 0471062596
Alfre'd Re'nyi. Probability theory
North-Holland Pub. Co.; (1970), 670 pages, ASIN: 0720423600
Neil J. A. Sloane, Florence Jessie MacWilliams
The Theory of Error-Correcting Codes
North-Holland; 9th reprint 1998 edition (January 1, 1983), 782 pages, ISBN:
0444851933
Физика
Общая физика:
Начальный курс:
Фейнмановские лекции по физике
Берклиевский курс физики
Савельев, Курс общей физики (в 3 томах)
Griffiths D. Introduction to (Electrodynamics, Quantum mechanics, Particle physics) замечательные книжки, но не переведены
Университетский курс:
Сивухин Д.В. Общая физика (5 томов)
Курс физики Матвеева.
Матвеев А.Н. Механика и теория относительности
Матвеев А.Н. Молекулярная физика
Матвеев А.Н. Электричество и магнетизм
Матвеев А.Н. Оптика
Матвеев А.Н. Атомная физика
В каждом томе есть упоминание, что она является каким-то томом курса физики, но в название нет этого самого номера тома. Всего их 5 томов.
Тамм И.Е. Основы теории электричества
Теоретическая физика:
George Joos, Ira Freeman. Theoretical Physics, Dover Publications, Inc. NY,1986.
Это 885 стр. и все в одном томе, прекрасное введение в теорфизику для 2-3-курсников.
Левич-Вдовин-Мямлин (Курс теоретической физики, в 2-х томах, 1962)
Ландау, Лифшиц все тома, как справочник (хоть и без индекса и без библиографии)
Теоретическая механика:
Начальное изучение:
Айзерман. Теоретическая механика
продвинутое изучение:
Арнольд. Математические методы классической механики (тут можно выучить всю
необходимую математику тоже! Изложение весьма математическое, стандартные задачи
типа "решить уравнения Гамильтона-Якоби для системы XYZ" отсутствуют напрочь.)
Ланцош. Вариационные принципы механики (как дополнение к Гантмахеру)
Гантмахер. Лекции по аналитической механике
Маркеев. Теоретическая механика
И. И. Ольховский "Курс теоретической механики для физиков".
Электродинамика:
Ландау и Лифшиц, том 2 (4-х мерные векторы и СТО уже надо знать)
Топтыгин. Современная электродинамика (?)
Батыгин, Топтыгин. Сборник задач по электродинамике
Джексон. Классическая электродинамика (3-е изд., 1998)
Гравитация:
Вайнберг. Теория относительности и космология
Квантовая механика:
начальное изучение
Ферми. "Лекции по КМ"
Блохинцев. "Основы КМ"
Дирак. Принципы КМ
Фейнман, Хибс. КМ и интегралы по траекториям
дальнейшее:
Коэн-Таннуджи и др. КМ двухтомник
Шифф. "КМ" (устарело)
Мессиа. "КМ" двухтомник
А. Б. Мигдал "Качественные методы в квантовой механике".
Ландау и Лифшиц, том 3 (не очень хорошие объяснения понятий, нет
ссылок на теорию представлений групп)
Петрашень, Трифонов "Применение теории групп в квантовой механике"
задачники
Галицкий-Карнаков-Коган
Елютин
Флюгге
Квантовая теория поля
для начального
Боголюбов, Ширков "Квантовые поля"+ "Введение в теорию квантованных полей"
Райдер, Квантовая теория поля (есть неотсканированное 2-е изд.)
Пескин, Шрёдер. Введение в КТП
Ициксон, Зюбер. КТП
Бьёркен, Дрелл. КТП
Список книг, заслуживших всенародное признание и любовь
В этом списке - книги, по которым мы учились и которые мы уважаем и ценим.
Эти учебники, по нашему общему мнению, существенно лучше многих других.
Звёздочкой отмечены книги, разыскиваемые в электронном виде. (Остальные уже
сосканированы.)
Рекомендации взяты из дискуссии, так что слово "я" это кто угодно.
Математика
Начальное изучение
"Числа и фигуры" Радемахера и Теплица
"Наглядная геометрия" Гильберта и Кон-Фоссена
"Что такое математика" Куранта и Роббинса
"Арифметика" Серра
Высшая математика
Мат. анализ, дифф. уравнения?
Рудин. Курс мат. анализа
Гурса, Кудрявцев, Никольский - разные курсы мат. анализа
Смирнов. Курс высшей математики
Петровский. Курс дифференциальных уравнений
Демидович. Задачник по мат. анализу
Филиппов. Задачник по дифф. уравнениям
А. Найфе "Методы возмущений". Необходимая книга после изучения мат.
анализа и дифф. уравнений, чтобы научиться считать асимптотики для точно нерешаемых задач.
ТФКП:
Ю.В.Сидоров, Федорюк, М.И.Шабунин. Лекции по ТФКП. (начальный)
Лаврентьев, Шабат. Методы ТФКП (более продвинутый)
Линейная алгебра:
Гельфанд. Лекции по линейной алгебре
Беклемишев. Лекции по аналитической геометрии (но плохо про тензорную алгебру!)
Очень простая со множеством примеров книжка по тензорному анализу
как первый учебник -
А.И. Борисенко и И.Е. Тарапов. Векторный и тензорный анализ с приложениями
(переведена на англ. и на западе пользуется большой популярностью, регулярно
переиздается в изд. Dover)
Дифф. геометрия и топология:
Стинрод, Чинн. Первые понятия топологии (школьный уровень)
Александров, Евремович. Топология
По топологии на западе считается одним из самым хороших учебников это
James R. Munkres, Topology. (2nd Ed включает общую и алгебраическую топологию)
Ясный стиль, тщательно подобраны примеры, продуманная структура изложения...
Могу лично подтвердить - лучше этой пока ничего не видал.
Дубровин, Новиков, Фоменко. Современная геометрия (физикам-теоретикам - особенно полезно)
Шварц. Квантовая теория поля и топология (это на самом деле книга по
алгебраической топологии, а не по физике, но очень хорошая)
"Теория Морса" Милнора
Spivak, Michael. A Comprehensive Introduction to Differential Geometry,
2ndEd. Berkeley, CA: Publish or Perish 1999 5 томов
B. O'Neil Elementary Differential Geometry, 2ndEd. (из всех западных
самое толковая и простая трактовка диф.геомет с объяснением смысла)
Функциональный анализ:
Линейная алгебра (подготовка к функану)
Глазман И.М., Любич Ю.И. Конечномерный линейный анализ в задачах.- М.: Наука, 1969.- 476с.
супер задачник по функану:
Кириллов А. А., Гвишиани А.Д. Теоремы и задачи функционального анализа. Изд.
2-е, перераб. и доп.-М.: Наука, 1988.-396 с.
еще по функану хорош Колмогоров-Фомин, а как подготовка -
матанализ по Рудину.
Мат. физика:
Арфкен. Методы математической физики
Чистая математика
Гриффитс, Харрис. Алгебраическая геометрия
Прикладная математика, численные методы
Price, Teukolsky, et al. Numerical recipes (хорошие объяснения методов, но
плохие программы к ним, так что писать программы надо самим
- методы также частично устарели, но всё равно как
вводный курс непревзойдённо)
Теория информации
Классика (значит "читал сам, постоянные ссылки в литературе"):
Robert G. Gallager
Information Theory and Reliable Communication
Wiley Text Books; (1968), 608 pages, ISBN: 0471290483
Thomas M. Cover, Joy A. Thomas
Elements of Information Theory
Wiley-Interscience; (August 12, 1991), 542 pages, ISBN: 0471062596
Alfre'd Re'nyi. Probability theory
North-Holland Pub. Co.; (1970), 670 pages, ASIN: 0720423600
Neil J. A. Sloane, Florence Jessie MacWilliams
The Theory of Error-Correcting Codes
North-Holland; 9th reprint 1998 edition (January 1, 1983), 782 pages, ISBN:
0444851933
Физика
Общая физика:
Начальный курс:
Фейнмановские лекции по физике
Берклиевский курс физики
Савельев, Курс общей физики (в 3 томах)
Griffiths D. Introduction to (Electrodynamics, Quantum mechanics, Particle physics) замечательные книжки, но не переведены
Университетский курс:
Сивухин Д.В. Общая физика (5 томов)
Курс физики Матвеева.
Матвеев А.Н. Механика и теория относительности
Матвеев А.Н. Молекулярная физика
Матвеев А.Н. Электричество и магнетизм
Матвеев А.Н. Оптика
Матвеев А.Н. Атомная физика
В каждом томе есть упоминание, что она является каким-то томом курса физики, но в название нет этого самого номера тома. Всего их 5 томов.
Тамм И.Е. Основы теории электричества
Теоретическая физика:
George Joos, Ira Freeman. Theoretical Physics, Dover Publications, Inc. NY,1986.
Это 885 стр. и все в одном томе, прекрасное введение в теорфизику для 2-3-курсников.
Левич-Вдовин-Мямлин (Курс теоретической физики, в 2-х томах, 1962)
Ландау, Лифшиц все тома, как справочник (хоть и без индекса и без библиографии)
Теоретическая механика:
Начальное изучение:
Айзерман. Теоретическая механика
продвинутое изучение:
Арнольд. Математические методы классической механики (тут можно выучить всю
необходимую математику тоже! Изложение весьма математическое, стандартные задачи
типа "решить уравнения Гамильтона-Якоби для системы XYZ" отсутствуют напрочь.)
Ланцош. Вариационные принципы механики (как дополнение к Гантмахеру)
Гантмахер. Лекции по аналитической механике
Маркеев. Теоретическая механика
И. И. Ольховский "Курс теоретической механики для физиков".
Электродинамика:
Ландау и Лифшиц, том 2 (4-х мерные векторы и СТО уже надо знать)
Топтыгин. Современная электродинамика (?)
Батыгин, Топтыгин. Сборник задач по электродинамике
Джексон. Классическая электродинамика (3-е изд., 1998)
Гравитация:
Вайнберг. Теория относительности и космология
Квантовая механика:
начальное изучение
Ферми. "Лекции по КМ"
Блохинцев. "Основы КМ"
Дирак. Принципы КМ
Фейнман, Хибс. КМ и интегралы по траекториям
дальнейшее:
Коэн-Таннуджи и др. КМ двухтомник
Шифф. "КМ" (устарело)
Мессиа. "КМ" двухтомник
А. Б. Мигдал "Качественные методы в квантовой механике".
Ландау и Лифшиц, том 3 (не очень хорошие объяснения понятий, нет
ссылок на теорию представлений групп)
Петрашень, Трифонов "Применение теории групп в квантовой механике"
задачники
Галицкий-Карнаков-Коган
Елютин
Флюгге
Квантовая теория поля
для начального
Боголюбов, Ширков "Квантовые поля"+ "Введение в теорию квантованных полей"
Райдер, Квантовая теория поля (есть неотсканированное 2-е изд.)
Пескин, Шрёдер. Введение в КТП
Ициксон, Зюбер. КТП
Бьёркен, Дрелл. КТП
очень продвинуто:
Вайнберг. Квантовая теория полей
Стритер, Вайтман. РСТ, спин, статистика и всё такое.
Также:
Швебер С. Введение в релятивистскую квантовую теорию поля.
Статистическая физика
Мне кажется самым лучшим введением в термодинамику и стат. физику является
Э.Ферми Термодинамика (должна быть до Ландавшица и других)
К. Хуанг. Лекции по стат. физике (есть 2-е изд.)
Ландау и Лифшиц, том 5
Кубо. Стат. физика
продвинутое изучение:
Климонтович. Статистическая физика
Квантовая теория твердого тела
начальный курс:
Ашкрофт, Мермин "ФТТ"
Киттель "Введение в ФТТ"
Займан "Электроны и фононы"
Анималу "Квантовая теория кристаллических твердых тел"
Ансельм "Введение в теорию полупроводников"
Хакен "Квантовополевая теория ТТ"
продолжение:
Киттель "Квантовая теория ТТ",
Давыдов "Теория твёрдого тела"
Физикам теоретикам необходимы также:
Д. А. Киржниц "Полевые методы теории многих частиц"
А. А. Абрикосов, Л. П. Горьков, Е. И. Дзялошинский "Методы теории поля в статистической физике"
Г. Я. Любарский "Теория групп и ее применение в физике".
Р. Маттук "Фейнмановские диаграмы в проблеме многих тел"
Дж. Займан "Принципы теории твердого тела".
У. Харрисон "Псевдопотенциалы в теории металлов".
У. Харрисон "Теория твердого тела".
И. М. Лифшиц, М. Я. Азбель, М. И. Каганов "Электронная теория металлов".
А. А. Абрикосов "Введение в теорию нормальных металлов".
*Slater J. C. Quantum theory of molecules and Solids, v.1, v2
McGraw-Hill, New York, 1965
Гидродинамика
начальное:
Лойцянский. Механика жидкости и газа
Ландау и Лифшиц, том 6 (?)
Зельдович, Райзер.
Лучшие школьные учебники и задачники
Глинка - Учебник химии
Киселев - Учебник геометрии
Козел М.С. и др. Сборник задач по физике (10 - 11 класс). "Просвещение", 2000
В.Г.Болтянский, Ю.В.Сидоров, М.И.Шабунин. Лекции и задачи по элементарной математике
Г.В.Дорофеев, М.К.Потапов, Н.X.Розов. Пособие по математике для поступающих в вузы
- они уже есть у СДБООМ, и вообще многое на СДБООМ неплохое. Кстати по
физике (верно ли мое мнение?) мне нравились
Е.И.Бутиков, А.Л.Быков, А.С.Кондратьев. ФИЗИКА ДЛЯ ПОСТУПАЮЩИХ В ВУЗЫ
Из очень хороших задачников по физике для продвинутых школьников я бы так же
рекомендовал:
Буховцев , Кривченков ,.. Сборник задач по элементарной физике 196Х
Гольдфарб Н.И. Сборник вопросов и задач по физике 197Х
Зубов, Шальнов. Задачи по физике 196Х
Ландсберг. Элементарный учебник физики
Это учебники по математике. Опять же ничего про них не знаю, за исключением
уважаемых фамилий Виленкина, Никольского, Погорелова.
I.
Учебно-методический комплект для 5-го и 6-го классов ( "ВИЛЕНКИН")
Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика. 5 класс Учебник.
Рудницкая В.Н. рабочая тетрадь по математике. No. 1, 2.
Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6 класс.
Учебник.
Рудницкая В.Н. Рабочая тетрадь по математике. No. 1, 2.
II. Г. В.Дорофеев и др. <<Математика>>. 5 - 9 классы.( "ДОРОФЕЕВ")
Новый учебный комплект представляет собой непрерывный курс математики для
5-9-х классов. В учебниках, содержание которых полностью
соответствует современным образовательным стандартам, учтены результаты
опыта преподавания математики последних десятилетий.
III.
Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Арифметика, 5.
Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Арифметика, 6.
Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Алгебра, 7.
Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Алгебра, 8.
Учебник являются первыми из серии <<МГУ - школе>>, инициатива создания
которой принадлежит Московскому университету им. М.В. Ломоносова,
заинтересованному в сохранении и развитии лучших традиций отечественного
образования.
IV. ("Нурк -Тельгмаа")
Нурк Э. Р., Тельгмаа А.Э. Математика : 6 - 9 классы
V ( "АЛИМОВ"
- Алгебра)
Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В., Федорова Н.Е., Шабунин М.И.
Алгебра, 7.
Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В., Федорова Н.Е., Шабунин М.И.
Алгебра, 8.
Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В., Федорова Н.Е., Шабунин М.И.
Алгебра, 9.
VI.("АТАНАСЯН" - Геометрия)
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.
Геометрия, 7-9.
Атанасян Л.С., Бутузов В.Ф., Глазков Ю.А., Юдина И.И. Геометрия: Рабочая
тетрадь для 7 класса.
Атанасян Л.С., Бутузов В.Ф., Глазков Ю.А., Юдина И.И. Геометрия: Рабочая
тетрадь для 8 класса.
Атанасян Л.С., Бутузов В.Ф., Глазков Ю.А., Юдина И.И. Геометрия: Рабочая
тетрадь для 9 класса.
или
Погорелов А.В. Геометрия,
7-9.
очень продвинуто:
Вайнберг. Квантовая теория полей
Стритер, Вайтман. РСТ, спин, статистика и всё такое.
Также:
Швебер С. Введение в релятивистскую квантовую теорию поля.
Статистическая физика
Мне кажется самым лучшим введением в термодинамику и стат. физику является
Э.Ферми Термодинамика (должна быть до Ландавшица и других)
К. Хуанг. Лекции по стат. физике (есть 2-е изд.)
Ландау и Лифшиц, том 5
Кубо. Стат. физика
продвинутое изучение:
Климонтович. Статистическая физика
Квантовая теория твердого тела
начальный курс:
Ашкрофт, Мермин "ФТТ"
Киттель "Введение в ФТТ"
Займан "Электроны и фононы"
Анималу "Квантовая теория кристаллических твердых тел"
Ансельм "Введение в теорию полупроводников"
Хакен "Квантовополевая теория ТТ"
продолжение:
Киттель "Квантовая теория ТТ",
Давыдов "Теория твёрдого тела"
Физикам теоретикам необходимы также:
Д. А. Киржниц "Полевые методы теории многих частиц"
А. А. Абрикосов, Л. П. Горьков, Е. И. Дзялошинский "Методы теории поля в статистической физике"
Г. Я. Любарский "Теория групп и ее применение в физике".
Р. Маттук "Фейнмановские диаграмы в проблеме многих тел"
Дж. Займан "Принципы теории твердого тела".
У. Харрисон "Псевдопотенциалы в теории металлов".
У. Харрисон "Теория твердого тела".
И. М. Лифшиц, М. Я. Азбель, М. И. Каганов "Электронная теория металлов".
А. А. Абрикосов "Введение в теорию нормальных металлов".
*Slater J. C. Quantum theory of molecules and Solids, v.1, v2
McGraw-Hill, New York, 1965
Гидродинамика
начальное:
Лойцянский. Механика жидкости и газа
Ландау и Лифшиц, том 6 (?)
Зельдович, Райзер.
Лучшие школьные учебники и задачники
Глинка - Учебник химии
Киселев - Учебник геометрии
Козел М.С. и др. Сборник задач по физике (10 - 11 класс). "Просвещение", 2000
В.Г.Болтянский, Ю.В.Сидоров, М.И.Шабунин. Лекции и задачи по элементарной математике
Г.В.Дорофеев, М.К.Потапов, Н.X.Розов. Пособие по математике для поступающих в вузы
- они уже есть у СДБООМ, и вообще многое на СДБООМ неплохое. Кстати по
физике (верно ли мое мнение?) мне нравились
Е.И.Бутиков, А.Л.Быков, А.С.Кондратьев. ФИЗИКА ДЛЯ ПОСТУПАЮЩИХ В ВУЗЫ
Из очень хороших задачников по физике для продвинутых школьников я бы так же
рекомендовал:
Буховцев , Кривченков ,.. Сборник задач по элементарной физике 196Х
Гольдфарб Н.И. Сборник вопросов и задач по физике 197Х
Зубов, Шальнов. Задачи по физике 196Х
Ландсберг. Элементарный учебник физики
Это учебники по математике. Опять же ничего про них не знаю, за исключением
уважаемых фамилий Виленкина, Никольского, Погорелова.
I.
Учебно-методический комплект для 5-го и 6-го классов ( "ВИЛЕНКИН")
Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика. 5 класс Учебник.
Рудницкая В.Н. рабочая тетрадь по математике. No. 1, 2.
Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6 класс.
Учебник.
Рудницкая В.Н. Рабочая тетрадь по математике. No. 1, 2.
II. Г. В.Дорофеев и др. <<Математика>>. 5 - 9 классы.( "ДОРОФЕЕВ")
Новый учебный комплект представляет собой непрерывный курс математики для
5-9-х классов. В учебниках, содержание которых полностью
соответствует современным образовательным стандартам, учтены результаты
опыта преподавания математики последних десятилетий.
III.
Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Арифметика, 5.
Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Арифметика, 6.
Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Алгебра, 7.
Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Алгебра, 8.
Учебник являются первыми из серии <<МГУ - школе>>, инициатива создания
которой принадлежит Московскому университету им. М.В. Ломоносова,
заинтересованному в сохранении и развитии лучших традиций отечественного
образования.
IV. ("Нурк -Тельгмаа")
Нурк Э. Р., Тельгмаа А.Э. Математика : 6 - 9 классы
V ( "АЛИМОВ"
- Алгебра)
Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В., Федорова Н.Е., Шабунин М.И.
Алгебра, 7.
Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В., Федорова Н.Е., Шабунин М.И.
Алгебра, 8.
Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В., Федорова Н.Е., Шабунин М.И.
Алгебра, 9.
VI.("АТАНАСЯН" - Геометрия)
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.
Геометрия, 7-9.
Атанасян Л.С., Бутузов В.Ф., Глазков Ю.А., Юдина И.И. Геометрия: Рабочая
тетрадь для 7 класса.
Атанасян Л.С., Бутузов В.Ф., Глазков Ю.А., Юдина И.И. Геометрия: Рабочая
тетрадь для 8 класса.
Атанасян Л.С., Бутузов В.Ф., Глазков Ю.А., Юдина И.И. Геометрия: Рабочая
тетрадь для 9 класса.
или
Погорелов А.В. Геометрия,
7-9.
Каким?


И как?
baka gaijin

Почему троллинг?
У меня очень много публикаций на дваче. И каждый день прибавляется. Вот и сейчас... пс: извените за неровный почерк.
Нуфаг начал вилять.

Какие исходные понятия в унивлаентных основаниях математики? Как они там определяют натуральные числа?
>striking formal resemblance to the Gaussian distribution
кек. а я вам говорил - изучайте umbral calculus. руку можно набить и любую неведомую хуйню вывести через совершенно другую, казалось бы не related хуету, немного подfudgить результат и готово - будет striking resemblance. good enough!
на mathoverflow есть норм разборы

>тут кто нибудь понял его теорию?
>тут
Лол, это такой юмор? Во всем мире ее поняли 4 человека (сообщили о том, что проверили мочизукины выкладки), ты думаешь, на этой параше сидят математики такого уровня? Фесенко (один из тех 4-х) пишет, что аспиранту-математику нужно около 10 лет, чтобы въехать в эту теорию, а специалисту, работающему в области теории чисел - примерно 500 часов.
>это такой юмор?
А тебе что - смешно?
Ведь общеизвестно что /sci - лучший научный форум на русском языке и следовательно - во всем мире
Определил тебе за щеку, проверяй корректность.
Только тщательно проверяй, а не как в прошлый раз языком работай.

Ты опять выходишь на связь? Тебе сто раз уже пояснили, N элементарно определяется в конструктивной теории типов https://en.wikipedia.org/wiki/Intuitionistic_type_theory
Маня, зачем ты притащил сюда интуиционистов если у них натуральные числа исходное неопределяемое понятие.
>>383792
Под шконку, гнида!
В прошлый раз ты был опущен и официально поулчил пробитый суповой набор.
>у них натуральные числа исходное неопределяемое понятие.
Схуяли? 0 - пустое множество, succ - функция следования, любое натуральное число - ординал. Нумералы Черча еще есть в лямбда-исчислении, слышал, нет?
> Схуяли
Интуиционизм по определению это направление которое исходит из интуитивного понятия натурального числа (или более обобщенно индукции). По их представлениям математические объекты и построения могут имеют право на жизнь только если сводятся к какой нибудь форме индукции, актуальные бесконечности они не рассматривают даже.
> 0 - пустое множество, succ - функция следования, любое натуральное число - ординал. Нумералы Черча еще есть в лямбда-исчислении, слышал, нет?
А как ты докажешь существование множества удовлетворяющего твоим условиям без индуктивных рассуждений? Я уже в прошлый раз заебался кнуёбку одно и тоже писать, что вы хоть читайте свои формулы, что за ними стоит, раскручивайте их до конца, до исходных понятий, прежде чем мне пытаться их впаривать. А то выпишут из вики набор символов, а как он получается даже не видели.
Решительно поддерживаю.
Поясните, а это говно нужно-ли кроме как для доказательства ABC-гипотезы? И, более сильно, нужно ли кому-то кроме теоретико-числовиков (тьфу-тьфу)?
Фесенко, по его поведению - типичный первокультурщик с двача, как в оппосте. Когда у них был устроен первый, провалившийся воркшоп чтобы совместно разобраться, математики из других стран слегка охуевали от тона его высказываний. Не удивлюсь, если нихуяшеньки он не понимает.
Кстати, что забавно, ученик Востокова.
Как минимум, это позволяет легко доказать или опровергнуть любое утверждение вроде ABC-гипотезы.
Анонасики, объясните как может быть математика без теории множеств? Множество это коллекция элементов, каких-то объектов. Но если мы оперируем хотя бы несколькими объектами, мы уже можем представить себе их коллекцию. Выходит все теории пытающиеся не использовать явно теорию множеств это всё херня?
Интересует литература по применению преобразований Фурье для решения дифференциальных уравнений с разрывными коэффициентами, но попроще классического Хермандера.
Боку но Бурбаку.
ты оперируешь не объектами, а выдумками
настоящая математика - это преобразование Дано в Ответ
Теория множеств — это про сорта бесконечностей, а не собрания объектов.
А про преобразование Фурье ты где читал? Поделись, пожалуйста.
Только в НМУ нет.
Нет. Теория порядковых чисел про сорта бесконечностей.
Фихтенгольцу они казались молодой сомнительной терминологией, и он предпочитал писать по-старинке.

Пока прочел лекции данилова из рэш, сейчас встал выбор: муллен, оуэн или петросян. Что лучше выбрать? или есть книжечки более достойные
По настроению.
До третьего, после запятой.
До второго апосля запетой.



Вкурил я значит Крауч, Старфилд - методы граничных элементов в механике твоердого тела. Короче первый пик, вроде понятно. На элементе задается пара известных проекций напряжений и смещений, причем в любой комбинации. Есть уравнения, по которым можно составить СЛАУ, если начальные условия неизвестны коэффициенты влияния A, B подставляем собственно как коэффициенты, если известны - произведение в качестве свободных членов. Сделал программу, даже посчитать что-то можно. Но вот как формировать СЛАУ для элементов высшего порядка, когда начальные условия задаются в узлах элемента, а не на самом элементе? Формулы то есть но нихуя все равно не понимаю.
Ок. Ты победил.
лол я это где-то читал но не помню хоть усрись. книжка кажись на инглише. это кажется переводик ее. но не помню. нахуя вообще что-то читать если потом не помнишь откуда. пиздос. пойду в дотку.
Че за говноедские коэффициенты?Ты повыебываться сюда пришел?Кури Лагранжа и не будешь больше спрашивать.

>Ты повыебываться сюда пришел?
Нет.
>Че за говноедские коэффициенты?
Геометрический контур тела разбивается на дискретные прямолинейные участки, на каждом из которых задаются напряжения\смещения. A,B - коэффициенты взаимного влияния напряжений\смещений для каждого из дискретных участков - граничных элементов. Верхний индекс - собственно индексы дискретных участков, нижний - проекции напряжений\смещний. Например, B - коэффициент влияния касательного (s) смещения i-ого элемента на касательное (s) напряжение j-ого элемента = Bijss. На втором пике - напряжения\смещения задаются не на элементе, а на узлах элемента, и соответсвенно индексы уже относятся к узлам, но так как один узел может относится к двум элементам - добавили еще индекс J элемента, собственно к которому узел и относится.
>>385138
Элемент пространства U + W имеет вид
(x + x, x + x, y + x, y + y).
Он просто переобозначил
x := x + x
y := y + x
z := y + y
>>385157
Неявно здесь имеет значение что умножение на двойку или сложение x самого с собой это сюръективная операция, поскольку F -поле. Именно поэтому мы можем сделать переобозначение, в произвольном кольце это не верно.
Сори, хуету написал. Т.е. сюрьективность тут важна, но другого отображения, а умножение на двойку не при чём. И всё будет норм в любом случае если в F есть ноль.

Ну это автор типа приводит древнее доказательство.
Спросил тоже. Тут никто не шарит в этой хуйне, все просто постят картиночки как оп дебил и задают вопросы. Особо отбитые просто умничают и толстят.
Предыдущий ОП (или может кто еще) немного разбавлял этот тред математикой, да.
Если его сопидору приснилась какая то хуйня это не мистика, а способ мышления, только и всего.
Допустим, мы сместим его вершины неким образом, но так, что длины сторон не увеличились.
Вопрос: как найти точку внутри преобразованного треугольника так, чтобы расстояния от неё до вершин были не более, чем p1, p2, p3 соотвественно?
Смещение треугольника - линейный оператор. Тебе нужно найти этот оператор в явном виде, затем подействовать им на твою точку.
Смотрю я на Бориса Сергеевича Бояршинова, и вижу себя двухлетней давности. Когда я впервые слушал Юрия Степановича Рыбникова. Вначале я улыбался над его словами, потом у меня были сомнения в психической вменяемости Рыбникова. И где то пол года мне надо было понять Величину Ума Юрия Степановича. За 24 минуты трудно понять Рыбникова. Но верю Борис Сергеевич умный человек и пройдёт эти стадии от скептицизма до того момента когда поймет с каким Великим Учёным он сегодня общался в живую. Мы ребята с YOUTUBA не пропускаем лекции Рыбникова и можно сказать являемся его заочными учениками. Он дал нам ответы на те вопросы, на которые ни родители, ни школа не могли ответить. Теперь нам не страшно, теперь Нам Жить хочется, я могу ответить на вопросы моего сына, которых великое множество БЛАГОДАРЯ ЮРИЮ СТЕПАНОВИЧУ РЫБНИКОВУ!
Ты дебил что ли? Я сказал: "Смещение ВЕРШИН треугольника". А не самого треугольника целиком.
Смещение вершин однозначно задаёт движение всей плоскости. Хотя зачем я тебе отвечаю.
Это законный способ упороться и словить трипы.
Да я серьезно спрашиваю....
Ты ебанутый?
Поворот = линейный оператор. Параллельный перенос - линейный оператор. Смещение - композиция поворота и параллельного переноса.
Что порешь, мудак? Ты можешь преобразовать один треугольник в другой линейным оператором? Дебил ебаный.
*sin^2(a)
Ебаный дебил, смести все три вершины треугольника независимо друг от друга одним поворотом и трансляцией. Сука тупой.

А о зависимости была?
Ты дурак что ли совсем наглухо?
Ну тот мемчик тебе всё правильно сказал, за исключением того, что отображение треугольника в треугольник задаёт не линейное, но аффиное отображение (линейное отображение + перенос). Тебе просто нужно взять образ твоей точки - эта точка будет как раз на тех же самых расстояниях от вершин что и исходная точка.
вот известная ебанина: 1+2+3+4+5+... = -1/12
можем ли мы сказать, что это просто тот момент, когда у вселенной наступает stack overflow?
Нет. С мистическими рассуждениями о вселенной - сразу нахуй.
>можем ли мы сказать, что это просто тот момент, когда у вселенной наступает stack overflow?
Нет.
Аффинное преобразование не сохраняет ни расстояния, ни их отношения.
Олсо, задачка бестолковая.
Уравнение второго порядка, т.е его решение y=C1 F1 + C2 F2 , где F1,F2 какие то функции x, а C1,C2 константы, вот в них и уходит граничное условие.
Вот например мне нужно найти решение уравнения, с помощью нигмы решение есть, но как найти тему с обьяснением, чтобы решать такие уравнения. Не искать же все уравнения подряд.
ty
3x−7+2(3−x)=−x+8
Но блин, как вообще искать тему, в которой рассказывают что это и как решать?
А сам как думаешь?
>Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:
>5x-2x=7+11
>(Чтобы лучше запомнить это правило, предлагаю следующую ассоциацию. Есть хозяин, к нему пришел гость. Хозяин у себя дома, в своих домашних тапочках. Гостю надо снять обувь, в которой он пришел — не будет же он ходить в доме в обуви, в которой ходил по улице.
>В левой части «хозяин» — слагаемое с переменной, 5x. Оно «у себя дома», поэтому его знак не меняем. «В гости» к нему приходит из правой части уравнения 2x. Его знак меняем на противоположный. В левой части 2x имело знак «+», при переносе знак изменяем на «-«.
>Аналогично, «хозяин» правой части — 7. Его знак не меняем, так как это слагаемое остается в правой части. К нему из левой части «приходит в гости» -11. Его знак меняем на противоположный — был «-«, при переносе меняем его на «+».)
>сектантов
Обоснуй за сектантов. MLTT и https://homotopytypetheory.org/ тоже сектантство? Уже даже основания изложили в интуиционистской форме.

Гугл молчит.
Если линейная часть аффинного преобразования сохраняла расстояния, то и аффинное сохраняет.
Может быть и может, вот только нахуя твои кусочно-картофанные образования, когда аффинные гораздо проще.

Так в чем сектантство-то, поясни. Ихние пруфы через пруверы - не пруфы или что?
Что ты пытаешься сказать? Не понимаю петушиный.

>>385788
>>385789
>>385790
Ясно всё с вами, маняматематики.
>Что вообще думаете за конструктивную математику, почему ее почти нигде не применяют кроме языков с зависимыми типами и пруверов?
Потому что её не существует?
Языков с зависимыми типами тоже не существует?
Проверяемая и корректная мат. модель чего угодно, из любой области знания. Все что угодно представимо в виде зависимого типа же.
Конструктивный объект на основе н-р рекурсивно перечислимых множеств и отношений, без всяких манябесконечностей.
>Проверяемый и корректный конструктивный объект на основе н-р рекурсивно перечислимых множеств и отношений, без всяких манябесконечностей чего угодно, из любой области знания. Все что угодно представимо в виде зависимого типа же.
Звучит уже не так впечатляюще.
Потому что ты не в курсе, что это вообще такое.
>Что вообще думаете за конструктивную математику
Когда узнал, что для того чтобы доказывать элементарные теоремы из анализа, требуется столько изъебств что ахуеть можно, понял, что это маргинальщина. Достойная существования, но форсить ее, такое себе занятие.
>пруверов
вообще считаю, это это первая весточка к смерти математики, так что в пизду и нахуй.
>вообще считаю, это это первая весточка к смерти математики, так что в пизду и нахуй.
А по 200+ лет доказывать всякие теоремы Ферма - это не смерть математики? 3,5 математика на всей планете въехали в теорию пространств Тейхмюллера ,это же ебаный стыд. Людишки не могут в математику, единственный вариант - переложить всю работу на комплюктеры. Теорему 4х красок именно так и доказали, к слову.
>для того чтобы доказывать элементарные теоремы из анализа, требуется столько изъебств что ахуеть можно, понял, что это маргинальщина.
А ты думал, поаутировал над бумажкой с ручкой и что-то доказал? Лол. Настоящая математика сложнее аутизма. Зато, все доказательства реально проверяемые.
Мимо имеющий публикации по конструктивной математике и руководящий проектом в австрийском университете.
>А по 200+ лет доказывать всякие теоремы Ферма - это не смерть математики?
Нет, это отдельные теоремы типа да/нет, ценность которых весьма сомнительна.
>Людишки
Мизантрап сациафаб?
>единственный вариант - переложить всю работу на комплюктеры
Ну то есть убить математику.
>Настоящая
Профессиональный математик закукарекал.
>>385817
>Читаю вас и аж умиляюсь.
То что ты примазался к своему научнику не делает тебе никакой чести.
>А по 200+ лет доказывать всякие теоремы Ферма - это не смерть математики?
Нет конечно.
>3,5 математика на всей планете въехали в теорию пространств Тейхмюллера
Пространства Тейхмюллера известны давным давно. Если это про Мочидзуку, то непонятные теории тоже были всегда, как и люди разводящие истерию на пустом месте.
Все это разговоры про компьютеры в 99% случаев бред людей, совершенно не понимающих что такое математика. Длинные формализованные доказательства сложных утверждений бессмысленны в принципе. Они нужны с единственной целью — узнать, что это можно доказать нормально.
То, что ты сразу проецируешь и гадаешь, только больше убеждает всех в твоей ущербности. О картофане пиздеть -- не реальные задачи решать.
Ахинея.
>Длинные формализованные доказательства сложных утверждений бессмысленны в принципе.
Хотел сказать, что вообще любые формализованные доказательства бессмысленны, длинные и сложных утверждений тут лишнее.
>въехали в теорию пространств Тейхмюллера ,
вьехать в эту "теорию" способен любой старшекурсник. В стекловке несколько раз читался курс лекций.
Давай ещё. Мне прям нравится.
>вот известная ебанина: 1+2+3+4+5+... = -1/12
Верная в рамках теории Р. Сколько аксиом в теории Р.? Порядка 50.
Можно построить теорию ХУЙ, где в качестве аксиомы мы возьмем 1+2+3+4+5+... = 0. Чем теория Р. лучше теории ХУЙ?
Ещё один логик.
>имеющий публикации по конструктивной математике
Макс, ты штоле? Ну хоть ты поясни. Выше вон говорят, что это сектантство. Я привожу пример HOTT, а это уже конструктивный вариант оснований, а не брауэровщина, про которую бурбаки писали, что это курьез, посмеяться сойдет. Так все равно говорят "ваши пруфы не пруфы".
Любой школьник по книге Тёрстона Трехмерная геометрия и топология. Он хотел выебнуться и сказать про интер-юниверсал, но запомнил только Тнйхмюллера. Странно что не Ходжа или Аракелова.
Аноны-математики, нужна ваша помощь. Поясните в общем про стереометрию и её факты, что-то необычное нужно.
Алгоритм Тарского. Лучше в вики посмотри насчёт фактов. Тебе для реферата что ли?
>Алгоритм Тарского.
Я посмотрел про него, но не понял.
>Лучше в вики посмотри насчёт фактов.
Смотрю вот.
>Тебе для реферата что ли?
Да, именно так.
Переведи статью с энвики и не еби себе мозги.
>про которую бурбаки писали, что это курьез, посмеяться сойдет
Срать на бурбаков.
>что это сектантство
Сектантство -- это верить во всезнающего оракула (аксиома выбора).
>Я привожу пример HOTT, а это уже конструктивный вариант оснований
И не только. Много чего. Например, констр. математика является основанием вычислимой математики math.andrej.com/data/c2c.pdf.
Кукареки местных детей про форм. верификацию меня вообще забавляют. Эта штука проникает буквально во все области, начиная от чистой теории и заканчивая чистой прикладухой, как софт и системы управления. Я могу ещё много рассказать, но зачем.
Если не влом, расскажи, что надо читать безнадежному тупому прикладнику, чтобы быть в тренде. На математика не претендую, но тема интеесна просто для общего развития. Должны же быть какие-то софт вей книжки, а-ля "вот что вы на самом деле должны были изучать на первом курсе"?
Не надо верить пропаганде сектантов-шизофреников. Адепты конструктивности недалеко ушли от РАЕН.
Если к чистой математике особых позывов и способностей нет, осваивай языки с зависимыми типами. Coq, Idris и так далее. Я когда-то, когда не был с ними знаком, проебал охуенную позицию в TUM по формальной верификации систем управления автономных машин через reachability analysis.
Ну и, если тебе ещё лет 17-20, поменьше слушай местное дерьмо вроде >>385926.
Кстати, а как конструктивисты относятся к аксиоме конструктивности? Вы её принимаете?

Привет смотрящим треда.
23 годика, в школе был отличником до 4 класса, после хер забил и преподаватель математики была злая бабка тварына + перевелся в другую школу и тд. Поэтому нихуя не учил, сейчас пытаюсь вкатится, но хрен там плавал, взял учебник за 5 класс, вроде простые уравнения порешал и понимание как это работает пришло, задачки на периметр тоже, а вот сейчас дошел до площадей прямоугольников, треугольников и прочего и обосрался, не могу сходу составить уравнение к задачке и решить. Это лечится вообще??
Например вот с подобным проблемы, стыдно даже показывать Периметр прямоугольника 6дм 8см, одна из его сторон на 1дм 6см меньше соседней. Найти площадь Пробовал khan academy совсем не то как-то.
>Периметр прямоугольника 6дм 8см, одна из его сторон на 1дм 6см меньше соседней. Найти площадь
Что такое "дм"?
1 дециметр = 10 сантиметров = 0,1 метр
>Периметр прямоугольника 6дм 8см, одна из его сторон на 1дм 6см меньше соседней. Найти площадь
Q. P=68, a=16. Find S?
Solution:
2a+2b=68
2⋅16+2b=68
2b=68-32
b=36/2
b=18
S=a⋅b=288
Solution:
2a+2b=68
2a+2⋅(16+a)=68
2a+32+2a=68
4a=36
a=9
b=25
S=a⋅b=225
> это верить во всезнающего оракула (аксиома выбора).
Сейчас бы в 2016, попридираться к аксиоме выбора.
>Эта штука проникает буквально во все области, начиная от чистой теории и заканчивая чистой прикладухой
Выхлоп то хоть какой-нибудь есть?
>Сейчас бы в 2016, попридираться к аксиоме выбора.
Не понимаю петушиный.
>Выхлоп
И опять же, не понимаю петушиный. Из какой деревни вы вылезли?

Допустим, про них я слышал, да, но это все-таки довольно специфическая тусовка, то есть, ну... блин, мне интересно что-то именно более математическое, но при этом не чистый дроч на самое себя, а более приземленное. И чтобы это все было изложено конструктивно. Вот что почитать в таком случае?
То есть не плт и цс тусовка, а обычная математика с тетрадкой и карандашом и картофанчиком^W^W - ну, надеюсь ты понял, о чем я.

ПМ кун врывается в тред, поссавши на селюка.
>матан начался
на двач он блять пошел, рэально, матан у него начался, а чего ожидал? ЕГЭ сдал и пиздец? Сосни ка ты хуица, ты блять здесь ревешь, а на функциональном анализе так ваще будет море крове, а до тензорного ты не доживешь.
Теперь все что ты можешь это похвастаться своими балами ЕГЭ перед такими же селюками, все пошел, небольшой расход и всех благ!
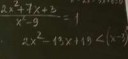
Полное решение напишите на листочке.
Нет, но забавно получилось.
c=x+y
b=a-c
k=-b
e=k-x
n=k+b
m=(n+c)-e
проверь выполняется ли при нули, правее нуля, левее нуля.
>>386027
Никто решение писать не будет, обращайся в спортлото.
Не понимаю петушиный. Пожалуйста, сформулируй мысль чётко.
Ну почитай Спиттерса.
Спасибо! Забыл, как мы это делали просто.
Японцы тоже Гитлера поддерживали, Мочидзука японец, надеюсь, ты понял о чём я!
>>386072
Дидывоевали головного мозга? Какая вообще разница, кем по жизни был тот Тейхмюллер? Главное - его вклад в науку же.

Суть такова: я буду заливать страницы со своей писаниной, любые комментарии приветствуются.
Курю зорича с начала, сейчас около конца главы о множествах. Решений в книжке нет и как вообще писать доказательства я хз не то чтобы знаю. Ну вы понели.
Начну заливать по реквесту, не хочу засорять хуйнёй тред, если всем похуй.
Зорич В.А. Язык естествознания. Математическая азбука.
Так же посоветуйте годные видео лекции по диффурам и
по преобразованиям лапласа, фурье
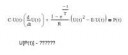
Ребят, помогите с уравнением (пикрилейтед), пожалуйста. Можно ли его вообще решить как хочу - U(P)? Или литературу порекомендуйте.
Я с Ухты
>его вклад в науку
Теорию саму разработал финношвед Алфорс и назвал оную в его честь. А сам техмюллер пошёл на фронт воевать против советов, где, собсно, и сдох.
в интернете купил:)
Ручка просвечивается через страницы люто, да и не стереть. Просто карандаш параша последнесортная, светлый и размазистый.
А в чем проблема? Там ответы в конце есть.
Директива #define создает макрос, представляющий собой ассоциацию обычного или параметризованного идентификатора со строкой токена. После определения макроса, компилятор может заменить строку токена для каждого вхождения идентификаторов в файле источника.
Во-во. Ты ввел в свой вопрос слова "площадь" и "прямоугольник на рисунке", однако не предоставил файлов с декларацией и дефиницией этих слов. Эти слова не являются зарезервированными ключевыми словами языка "Математическая теория T".
Cоси, анус тоже подставь.
>>386366
Тебя это ебёт, блядь? Решай или не решай, к чему эти вопросы идиотские.
инб4: ололо школьнег))
Пруф?
Теорией множеств, комбинаторикой и линейной алгеброй не решить. Элементарными в любом случае.
Это раздел для детей с отставанием в развитии?
4562?
Решал довольно таки в лоб, мог где-то в рассчетах провтыкать, порядок цифр хотя бы сходится?
На все про все ушло 15 минут.
Мимо не математик
Он один из немногих работающих в РАН докторов наук, которые имеют звание "почетный профессор", если тебе это что-нибудь говорит.
Я на него всегда смотрел, и понимал, что он охуенный, и что он это я, и что я бы обязательно так и читал, если бы делал научную карьеру, а не ушел бы в мистику, наркоманию и алкоголизм.
Но с другой стороны, если бы я не ушел в наркоманию, а делал бы научную карьеру, то я бы так не читал, а был бы обыкновенным скучным хуем.
Парадокс в общем. Но мужик заебись.
Потому что дохуя сделал. Обычный доктор наук всю жизнь работает, чтобы получить хотя бы один заметный другим людям результат, Рома же убер-сайенс куёт как из печки.
https://scholar.google.ru/scholar?q=Mikhailov+roman
Посмотри на цитирования. Этот чувак умнее Шелдона.
А ещё он жонглёр, наркоман, индуист и в детстве гопал прохожих по ночам.
Ты спрашивал?
Может унизить сосачеров на любом поприще.
>Ещё по составлению списков не унизит.
А вот тут я думаю ты не прав. Он как раз начал в своей жежешечки составлять списки.
Пиздец, а я решил все задачи от туда уже, в следующей понедельник пойду сдавать. А с чем у тебя проблемы? Какой лвл, что заканчивал, чем сейчас занимаешься?
Взрослый я. Что заканчивал не скажу, ибо диванон.
А ты глаза открой и оглянись. В топах чартов музыки - говно и отбросы. Громадную часть сборов получают 2.5 мужика и теория бозонги. Каждого первого философа и человека искусства отторгают как только могут если он впереди своего времени - потому что такие люди время и двигают, жертвуя собой. Инновациям в науке научное же сообщество и противостоит.
А в наше время к этому добавляется еще и слепая система, допускающая до рабочих позиций только счастливых единиц, и то в основном за счет связей и денег. Вот и прибавь два и два, какой шанс даже у очень одаренного человека пробиться? Хоть новую фундаментальное взаимодействие открой, если и опубликуешься, статья может потонуть в тоннах китайского высера, которым эти зерги заспамливают науку.
> Маня сопоставляет науку и поп-музыкантов
Мань, напрягаешь булки, берёшь, пишешь статью чётким научным языком, отправляешь, получаешь ревью, пишешь ответы и исправляешь ошибки, сжав челюсти от баттхёрта, который неминуем, может быть, публикуешь спустя год, а потом выёбываешься тут про непризнанных гениев и какая гнилая система. Только вот, скорее всего, после публикации тебя такой детский сад уже перестанет интересовать

Хотя ладно. Признаюсь. ФМЛ при ПТУ им Дауна я заканчивал, а потом и сам ПТУ вот специальность и лвл не скажу, кекеке.
В итоге ответственно заявляю: уровень математики в хваленой Даунке - крайне низок. С той же абстрактной алгеброй в итоге я там так ни разу и не встретился, а линейка была уровня говна и палок без задач буквально пару лет назад узнал ее практическое применение. Зато красиво шрифты в чертежах карандашами рисовать до сих пор умею.

Прост тебе, школотрон, какая разница, что я там буду делать? Я в отличие от тебя это буду делать хотя бы осознанно.
Держу пари, ты ни одной не опубликовал. Разве что в сборнике трудом одарённых студентов Петрозаводского Заборостроительного.
Я чем-то тебя задел? Мне интересно, кто туда ходит и почему --- это делает меня плохим?
Ну заебись, на следующую лекцию такие как ты не придут и я хотя бы зайти смогу. А еще через пару недель может даже сидячие места появятся.
Он в своём жж писал, что хочет познакомится, на лекциях Вербита (пространства модулей, что-то там...) прямо онлайн на Лекториуме замечен (по крайней мере мне так показалось), они друг друга неиллюзорно уважают.
Еще не смотрел. По алгебре все решил.
В отличие от тебя я давно работаю и физически на лекции оказаться не могу. Но в 2016-м году существует такая штука, как интернет, где есть сайт НМУ, где выложены все лекции и материалы
Объясни мимокроку, это ты так хитро постебался, или такие кол-ва цитирований действительно являются чем-то выдающимся у мочематиков?
У серого хуесоса так сраку порвало, что он уже третий раз подряд неверно детектирует меня в трех разных анонах. Продолжай болтыхаться, доставляет.
А кто круче, самурай или ниндзя?
Нет, искренне интересуюсь. В естественных науках вроде физики такими числами никого не удивишь. В всяких космологов или биологов так вообще рассмешишь.
Да, для математиков такое количество цитирований ненормально велико.
Я тоже работаю, но у меня гибкий график, я ж не быдло. на самом деле быдло, но не настолько, чтоб у меня был фиксированный рабочий день
Anybody?
Упорядоченная пара - это {{x}, {x,y}}. Соответственно, выделять её нужно из булеана булеана объединения. Булеан объединения даёт {x} и {x,y}, булеан булеана - саму пару.

На самом деле упорядоченная пара это любая неупорядоченная пара, в которой один элемент обладает эксклюзивным свойством, по которому ему можно придать номер.
Я почему спрашиваю. У меня в зориче предлагают из булеана объединения булеанов сделать.
В Зориче известная опечатка, на неё Зоричу пеняют уже много лет. Даже Вавилов в своих конкретных множествах по ней проехался. Хотя на самом деле там можно что-то сделать с аксиомой замены, так что не такая уж это и опечатка. Но речь, вообще, о P(P(XUY)).
ниибу
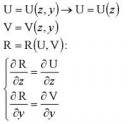
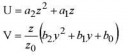
(Df)X(∆) = X∆ + ∆X?
Можно подробнее? Я тоже размышлял на тему восстановления функции по ее полному дифференциалу. Но, к сожалению, само выражение не задано.
Представь себе кривую лежащую в плоскости. В каждой точке кривой проводим нормаль к кривой и на нормали откладываем отрезок заданной длины, соединяем все найденные точки - получаем кривую. Есть ли у этой кривой название?
Эквидистанстная деформация, может быть? (Громов, Знак и геометрический смысл кривизны)
К сожалению не лекции а лекция. И последующие почему-то не выкладывают. Вообще есть какой-нибудь способ воздействия на этих пидоров из Лекториума?
>пидоров из Лекториума
Единственные нормальные люди на всю Россию, которые делают что-то полезное. В отличии от криворуких ВШЭ и НМУ даунов. Снимают четко, ровно, звук хороший, свет нормальный, лекторы замечательные. Одним словом петербуржцы. Но сосачеры все равно недовольны.
Ну я согласен с твоими аргументами, но это не отменяет того что они пидоры и могут задерживать выпуск лекций месяца на три.
>НМУ даунов
Кстати вот двачую, много раз хотел посмотреть их лекции, но НМУ-перхоти всегда удавалось отговорить меня - то лекции проёбаны, то половина файла битая, то на половине лекции звука нет. Короче да, среди всех Лекториум - самый нормальный.
Иногда лучше ничего.
нахуй тебя пидора, учил гомологии по нему, читал его перевод хатчера - ЗА ЕБ ЦА, ты даун ебаный просто
Прасолов в треде.
Подскажите кто нибудь, как именно искать первообразный корень по модулю простого числа.
А то после функции Эйлера в показателе степени, ничего непонятно...

Первообразным корнем по модулю n (primitive root modulo n) называется такое число g,
что все его степени по модулю n пробегают по всем числам, взаимно простым с n.

a^phi(n) === 1 mod n; где a - первообразный корень по модулю числа n

1. Берем простое число n.
2. Вычисляем функцию Эйлера. phi(n) = n-1, если n простое.
3. Факторизуем, т. е. раскладываем phi(n) из функции Эйлера на простые множители.
4. Перебираем a от 1 до n и для каждого из них считаем:
a^(phi(n)/Pi) mod n, где Pi - P1P2P3*P4, множители факторизованного числа из функции Эйлера.
5. Если, для текущего a ВСЕ ЭТИ числа оказались отличными от 1, то a является искомым первообразным корнем.

a называется порождающим элементом или генератором, зерном, seed.
При возведении a в различные степени по модулю p - получаем равномерное распределение результатов.
>>388644
>p
n fix;
Просто оставлю это здесь:
http://kaf401.rloc.ru/Criptfiles/primroots.htm
Но как искать первообразные корни из непростого числа n? По этому же алгоритму?
Их много, и вот DOC https://vk.com/doc1604842_312389462?hash=67c5c826783cface5d&dl=6fb26cd5da7826f116
Правильно и своевременно попадать в условия, в которых всё это нужно, для выработки условнорефлекторных связей в белом веществе, в мозгу.
Мне всегда было интересно мотивировка всего этого. При исследовании чего это было найдено?
Ты истории не знаешь. Не умер. Его жиды убили.
Что почитать из математической статистики? Чтобы понятно и доступно для неискушенных всякие распределения объяснялись?
Первообразные корни надо чтоб засидить генератор на равномерное распределение. Очевидно же.
Отучился на эту хуету, ушёл гамалогии теребить, всяко интереснее.
Сделай давай, чё языком то молотишь. А когда поймёшь, что даже тривиальные утверждения приходится доказывать крайне сложными доказательствам,да ещё ис помощью хер знает как сделанных УНИКАЛЬНЫХ и НЕ ИМЕЮЩИХ АНАЛОГОВ пруверов - тогда займёшься более адекватной математикой.
Ну а так, это всё очень хорошо, я всеми лапками за эти начинания, но там высокий порог вхождения, высокая сложность, и, соответственно движется дело медленно. Уж 30 лет назад mltt был.
проорал с пикчи
Ты там далеко не один из этой шараги, поуважительнее относись, а то о нас не очень хорошо будут думать.
Так таки есть какие-нибудь элементарные прикладные штуки на этом языке? Геометрия элементарная, блждад, написана кем-нибудь в рамках этого?
Просвети, милый друг. Что мне надо узнать, чтобы изменить мнение? Я только рад буду.
Я достаточно длинные доказательства писал на этом хотте. Это тот ещё мучительный процесс. Не только от того, что тупо долго и объёмно, а из-за того, что хз: завтра синтаксис изменится и я обосрусь со своим доказательством. (Соякова так попадала, например)
Мне б ещё какую-нибудь методу, чтобы понимать, как оно там внутри среды устроено...
Так уже предложили доказать какую-нибудь тривиальную теорему, навроде "основная теорема чего-либо", но это судя по всему еще недоступно.
x - голосуют. Влияние - 100/x. 1% = 1/100 ⋅ 100/x = 1/x;
y - отбирается из x; k = x/y; x = ky; Влияние голоса 100/y. 1% = 1/y = k/x;
Да, и там ещё зависимость от вероятности, вроде, потому что купленный из числа x может войти в y, а может и не войти.
А сразу несколько купленных x могут гарантированно оказаться в числе y.
Короче, количество купленных дядек с вероятностью коррелирует, походу.
> k = x/y
Что такое k?
>1% = 1/y
Это не 1%.
>>389021
Вероятность не важна. На больших числах распределение всё исправит и погрешнасть будет небольшая. Плюс там принцип дирихле не учитывается т.к. больше 50% набирать не надо.
>теория Р
Что это? Я думал в математике всего 2 аксоимы. Про натуральные числа и операцию сложения. А остальное это их следствие.

Можно по нему гамалогии выучить?
>Что такое k?
>k=x/y это коэффициент проходимости
Это - твоё.
>1% = 1/y
>Это не 1%.
Да, это я влияние голоса на 1% перемножил, с дури.
x - участвуют;
pr = 1; нужный процент;
g = 100/x; влияние одного голоса;
ob = g/(pr/100) - влияние голосов, для нужного процента.
chel = x ⋅ g/(pr/100) - влияние к-во чел, для нужного процента.
>Вероятность не важна.
А если из 1000000 человек отбираются 100?
>Какие ещё есть способы?
НЛП, без подкупа. Проверка аргументации.
Отслеживание взаимодействия с заинтересованными лицами, отстранение от голосования по этим причинам.
Тотальный контроль целесообразности и автоматизация.
Покажи кусок

Ты думаешь TRUE? А вот и FALSE.
Ты думаешь FALSE? А вот и TRUE.
Ты думаешь TRUE, и полагаешь что FALSE? И TRUE и FALSE, одновременно.
Ты думаешь FALSE, и надеешься что TRUE? И не TRUE, и не FALSE, одновременно.
Думаешь это всё по отдельности? А это всё ещё и вместе. И в динамике.
>Это - твоё.
Моё всегда меньше единицы. Это y/x.
>>389109
g = 100/x; влияние одного голоса;
g сразу в процентах? Может быть путаница с другими формулами.
>ob = g/(pr/100) = 100/x*100 = 10000/x
А вот и путаница.
>>389109
>chel = x ⋅ g/(pr/100) - влияние к-во чел, для нужного процента.
Смотри ка. Константа.
>А если из 1000000 человек отбираются 100?
Отбирают рандомно. По статистике процент попадания не должен сильно изменится если выбирают 1000 из 10000000.
А нормальные математические методы есть?
>Хули ты, тогда:
Опечатка в функции её исправил.
>ob = pr/100 [1], общее влияние.
ob = g/(pr/100) = 1/чел/контанту
chel = чел * 1/чел = 1
Этот способ доказано не работает. Другой помогите придумать.
>g сразу в процентах? Может быть путаница с другими формулами.
Да.
g = 1/x ⋅ 100% = 100%/x [%/чел ≠ 1/чел];
>f(x,y)=1/(100kg)
Что ты делаешь тут?..
k = y/x;
y = k⋅x;
g_x = 1/x;
g_y = 1/y = 1/(k⋅x);
k⋅g_x = k/x;
k⋅g_y = k/y = 1/x;
ob = pr/100 [%/100 = 1], же, не g/(pr/100).
>Что ты делаешь тут?..
k это коэффициент людей которые будут отобраны из x в y. g это вес голоса каждого из этих людей. перемножим их получим коэффициент для перевода количества купленных людей в количество купленных процентов голосования. 100 чтобы перевести в проценты. Деление на 1 т.к. нам нужен только 1 процент.
>k⋅g_y = k/y = 1/x;
Правильно. Теперь подставить в f(x,y)=1/(100kg). Получим x/100. y сократился. Вот и доказательство что метод не работает.
В графическом методе разобрался, после симплекса надо будет найти базис и решить двойственную задачу.
Всё для университета. Так вот, к чему я.
Вот смотрю лекцию в интернете, по решению симплекса и не могу понять а в чем разница при вычислениях, если минимум и максимум отыскивается? Ну вот что-то это не упоминается. И в интернете не могу нагуглить разницу.
Заранее спасибо, надеюсь что кто-то из вас разбирается в симплексе.
>g это вес голоса каждого из этих людей.
Каждого из y?
> количество купленных процентов голосования.
Считай лучше доли, а то с этими процентами долбануться можно.
x = 1000000, участвуют.
g_x = 1/x = 1/1000000 = 0,000001, вес каждого из x.
y отбирается из x;
y = 1000, отобранные.
k = y/x = 1000/1000000 = 0,001; коэффициент
y = kx;
g_y = 1/y = 1/1000 = 0,001, вес каждого из y;
pr = 2,5, процент.
d = pr/100 = 2,5/100 = 0,25, доля подкупных.
kol_x = x⋅d = 1000000⋅0.025 = 25000, количество подкупных из x;
kol_y = y⋅d = 1000⋅0.025 = 25, количество подкупных из y;
kol_y = k⋅kol_x = 0,001⋅25000 = 25;
>перемножим их
k⋅g_x = 0,001⋅0,000001 = 0,000000001, хрень какая-то.
k⋅g_y = 0,001⋅0,001 = 0,000001 = g_x, такие дела.
>получим коэффициент для перевода количества купленных людей в количество купленных процентов голосования.
>100 чтобы перевести в проценты.
100k⋅g_x = 0,000000001⋅100 = 0,0000001, хрень какая-то.
100k⋅g_y = 0,000001⋅100 = 0,0001, тоже непонятно что.
1/100k⋅g_x = 10000000, хрень какая-то.
1/100k⋅g_y = 10000, ещё большая хрень.
Потому что 25000 подкупных из x, и 25 из y.
>g это вес голоса каждого из этих людей.
Каждого из y?
> количество купленных процентов голосования.
Считай лучше доли, а то с этими процентами долбануться можно.
x = 1000000, участвуют.
g_x = 1/x = 1/1000000 = 0,000001, вес каждого из x.
y отбирается из x;
y = 1000, отобранные.
k = y/x = 1000/1000000 = 0,001; коэффициент
y = kx;
g_y = 1/y = 1/1000 = 0,001, вес каждого из y;
pr = 2,5, процент.
d = pr/100 = 2,5/100 = 0,25, доля подкупных.
kol_x = x⋅d = 1000000⋅0.025 = 25000, количество подкупных из x;
kol_y = y⋅d = 1000⋅0.025 = 25, количество подкупных из y;
kol_y = k⋅kol_x = 0,001⋅25000 = 25;
>перемножим их
k⋅g_x = 0,001⋅0,000001 = 0,000000001, хрень какая-то.
k⋅g_y = 0,001⋅0,001 = 0,000001 = g_x, такие дела.
>получим коэффициент для перевода количества купленных людей в количество купленных процентов голосования.
>100 чтобы перевести в проценты.
100k⋅g_x = 0,000000001⋅100 = 0,0000001, хрень какая-то.
100k⋅g_y = 0,000001⋅100 = 0,0001, тоже непонятно что.
1/100k⋅g_x = 10000000, хрень какая-то.
1/100k⋅g_y = 10000, ещё большая хрень.
Потому что 25000 подкупных из x, и 25 из y.
>Каждого из y?
да
>>389144
>Считай лучше доли, а то с этими процентами долбануться можно.
Дам везде доли коэффициенты и тольк 1 раз проценты т.к. результат голосования в них измеряется.
>k⋅g_x = 0,001⋅0,000001 = 0,000000001, хрень какая-то.
g для x считать не надо
>k⋅g_y = 0,001⋅0,001 = 0,000001 = g_x
Это следовало из той функции.
>тоже непонятно что
Это сколько я получу процентов голосования получив 1 голос. если купить 25к голосов, то получи 2.5 процентов. Пусть этот коэффициент будет a, а я хочу p процентов накрутить и для этого мне нужно купить f(x,y) голосов. Поэтому f(x,y)*a=p. По определению p=1. Поэтому f(x,y)=p/a
>>389144
>1/100k⋅g_x
Это для одного процента. >>389011
> Функция f принимает x и y, а возвращает количество человек которых нужно подкупить чтобы получить 1% от общего числа голосов
>>389151
Случайно отправил не весь пост
>g_x = k⋅g_y = 0,001⋅0,001 = 0,000001
>f(x,y)=1/(100kg) = 1/100⋅g_x
>g для x считать не надо
>Это для одного процента.
10к⋅2,5 = 25к, да.
Но ты вопрошаешь о способе увеличения количества подкупных для изменения результатов...
Способ, который ты выбрал - просто сужать круг участвующих в голосовании, рандомной выборкой в y. Но если из общего фона в 1Мегачел уже куплено 25килоизбирателей - этот фон уже искажён. Такие дела.
Ага. Это я сказал в первом посте. А ещё спросил как увеличить количество человек коорых нужно купить без увеличения x

И менять их так быстро, чтобы при попытке подкупить - не успели ещё. А количество подкупленных - считать. Или отслеживать движения их баблища. Можно жучков напихать в телефон, и снифферами обвесить коммуникационные каналы. В обменнике валюты майора поставить, а нал метить. Лол.
Разве что, по личной целесообразности выбора кандидата, для каждого. Тогда психологов напихать избирателям.
Нет. Надо математически найти решение или доказать что его нет.
Гугл никак не помог.
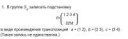

Бросил математику в 18 лет, до этого был, ну богом не богом, но до международочки в школе все же добрался. Дальше девяностые, в общем как-то было не до того, много важных дел - бухать, торчать, ебаться, читать Кастанеду и упарываться осознанными сновидениями, наверное из-за этого и не деградировал, потому что мистика все же довольно тяжелый труд.
Сейчас попробовал вернуться в математику - двойственное ощущение. Во-первых, понимаю, насколько мои знания находятся на уровне каменного века, с другой стороны, когда пробую всякие университетские задачники, то там довольно смешной уровень, все эти задачи со звездочками ложатся передо мной как блудливые телки перед мачо.
Как считаешь, анончик, есть у меня перспективы на средней руки науку? На серьезную, конечно, не претендую, все же возраст уже чуть не тот, 35+ ранг и налысо забрит.

Давай проверим. Вот задача пикрелейтед. Перечисли как можно больше разных её решений.
Нет. В среднюю науку без аспирантуры не пустят.
Сейчас нереально в 18 лет прорыв в науке сделать, слишком далеко все ушло. Это даже оставляя в стороне тот вопрос, что я не Галуа.
Ну смотри, тебе нужна академическая степень. Сложность ее получения и есть путь к средней руки науке.
Ну для начала.
1) Сперва закрашиваем все отрезки вида [2n, 2n+1] и сводим задачу к заполнению открытого промежутка, который скопируем на все промежутки вида (2n-1, 2n).
Промежуток длиной один закрашиваем скажем по методу канторовой пыли.
Я правильно понял условие? Это считается решением?
Лол, только вчера друзявки рассказывали, у нас жопа в городе, на факультет классической математики зачислились три человека. Скорее всего будут его сливать с чем-то, только неясно с чем.
Давайте я к вам приеду, зачислюсь. Там точно классическая математика? Без всякого этого говна со множествами?
Прежде чем я переселился в наливайку за углом, смутно помню какие-то сечения, так что у меня для тебя плохие новости.
Аксиому выбора вот правда не припоминаю. Так что если ты противник зфц то можешь рискнуть.
Не надо, я платонист.
>>389277
О, ну хотя бы так! Хорошо, как мне получить гражданство? Я слышал, там какая-то речка есть, и там мостик заброшенный, и вот там-то все границу и переходят. Ты меня проводишь? Но только если и впрямь никакой зфц!
Лети в Молдавию, там пойдешь на конспиративную квартиру, пароль Пеано. Тебя посадят на автобус, сам ни с кем не заговаривай, на все вопросы отвечай: entschuldigung, ich verstehe deine barbarische Sprache nicht. Когда начнется дорога как после бомбежки, значит ты уже почти на месте.
Если увидишь в окне портрет Кантора, ни в коем случае не заходи, явка провалена.
Сдается мне, ты меня морочишь, и других решений нет.
Старого бедного человека морочишь, который не учил топологию, не стыдно тебе?
Ладно, принимаю твой вызов, попытаюсь обойтись средствами матана и теории множеств, в крайнем случае докажу, что принципиально других решений нет.
Итак, для начала, белых отрезков не более чем счетное количество, потому что их не более чем счетное количество на любом отрезке длиной 1, потому что если нумеровать их на этом отрезке по убыванию длины, то отрезок длиной 1/n или больше не может стоять дальше чем на месте n. Все верно излагаю?
Хехе.
Придумал вот забавное разбиение, так, чтобы суммарная длина белых отрезков была вообще конечной, и сколь угодно малой.
Занумеруем все рациональные числа по возрастанию суммы числителя и знаменателя. Возьмем заранее число x. На каждом шаге делим x на два, берем новое рациональное число, если оно уже на белом отрезке то ок, идем дальше. Если нет, то рисуем белый отрезок длиной x с центром в этой точке, при необходимости делим еще пару раз на 2, чтобы не пересекался с другими отрезками. Итого, в итоге, все рациональные числа покрашены в белый цвет, суммарная длина отрезков не больше 2*x.
Другие решения есть. Вот моё, например. Рассмотрим всевозможные множества попарно непересекающихся отрезков, упорядочим их по включению, применим лемму Цорна.
Ничего не понял, разъясни поподробней, как ты получаешь финальный набор отрезков? Ну и кроме того, эти множества по включению ты сможешь упорядочить лишь частично.
Множество называется частично упорядоченным, если на нём задано рефлексивное, антисимметричное и транзитивное отношение <=.
Пусть множество M частично упорядочено.
Пусть A - его подмножество.
Если любые два элемента A сравнимы между собой, то A называется линейно упорядоченным подмножеством M, или цепью в M.
Пусть M - частично упорядоченное множество, пусть A - подмножество в M, пусть x - элемент M. Если для любого a из A верно, что a <= x, то x называется мажорантой для A. Мы говорим, что множество мажорируется, если оно имеет хотя бы одну мажоранту.
Пусть M - частично упорядоченное множество. Пусть m - его элемент. Мы говорим, что x является максимальным элементом в M, если для любого x из M то, что m<=x, влечёт m=x.
Лемма Цорна. Если в частично упорядоченном множестве M любая цепь мажорируется, то в M существует хотя бы один максимальный элемент.
Пусть M - семейство всех множеств попарно непересекающихся отрезков прямой. Элементами M, подчеркну, являются не отрезки, а множества отрезков. Упорядочим M по включению. Если a,b - элементы M, то a<=b титтк a - подмножество b.
Пусть A - цепь в M. Пусть B - объединение A.
Докажем, что B - элемент M.
Элементами B являются отрезки.
Пусть p,q - элементы B.
Существуют такие P и Q из A, что p∈P, q∈Q.
Так как A частично упорядочено, либо P⊂Q, либо Q⊂P.
Без ограничения общности будем считать, что p,q - элементы P.
Тогда p и q не пересекаются.
То есть B состоит из отрезков, которые попарно не пересекаются.
Что и требовалось.
Далее, ясно, что B мажорирует A, - любое множество из A является подмножеством B.
Таким образом, любая цепь A в семействе M мажорируется множеством ∪A. По лемме Цорна, в M существует хотя бы один максимальный элемент. Обозначим его S.
Множество S - семейство попарно непересекающихся отрезков прямой. Покрасим его в белый цвет. Если есть отрезок прямой, на котором нет ни одной белой точки, то мы могли бы добавить его в S, - что противоречит максимальности S.
Множество называется частично упорядоченным, если на нём задано рефлексивное, антисимметричное и транзитивное отношение <=.
Пусть множество M частично упорядочено.
Пусть A - его подмножество.
Если любые два элемента A сравнимы между собой, то A называется линейно упорядоченным подмножеством M, или цепью в M.
Пусть M - частично упорядоченное множество, пусть A - подмножество в M, пусть x - элемент M. Если для любого a из A верно, что a <= x, то x называется мажорантой для A. Мы говорим, что множество мажорируется, если оно имеет хотя бы одну мажоранту.
Пусть M - частично упорядоченное множество. Пусть m - его элемент. Мы говорим, что x является максимальным элементом в M, если для любого x из M то, что m<=x, влечёт m=x.
Лемма Цорна. Если в частично упорядоченном множестве M любая цепь мажорируется, то в M существует хотя бы один максимальный элемент.
Пусть M - семейство всех множеств попарно непересекающихся отрезков прямой. Элементами M, подчеркну, являются не отрезки, а множества отрезков. Упорядочим M по включению. Если a,b - элементы M, то a<=b титтк a - подмножество b.
Пусть A - цепь в M. Пусть B - объединение A.
Докажем, что B - элемент M.
Элементами B являются отрезки.
Пусть p,q - элементы B.
Существуют такие P и Q из A, что p∈P, q∈Q.
Так как A частично упорядочено, либо P⊂Q, либо Q⊂P.
Без ограничения общности будем считать, что p,q - элементы P.
Тогда p и q не пересекаются.
То есть B состоит из отрезков, которые попарно не пересекаются.
Что и требовалось.
Далее, ясно, что B мажорирует A, - любое множество из A является подмножеством B.
Таким образом, любая цепь A в семействе M мажорируется множеством ∪A. По лемме Цорна, в M существует хотя бы один максимальный элемент. Обозначим его S.
Множество S - семейство попарно непересекающихся отрезков прямой. Покрасим его в белый цвет. Если есть отрезок прямой, на котором нет ни одной белой точки, то мы могли бы добавить его в S, - что противоречит максимальности S.
>Элементами B являются отрезки.
Разве?
Пусть множество Аn состоит из всех отрезков вида [a+1/n, a+1-1/n], где а пробегает множество натуральных чисел, а n - фиксировано для данного An.
Аn - цепь, но объединение B всех An не есть элемент M, оно состоит из открытых интервалов (n, n+1), то есть из прямой с выколотыми натуральными точками.
Если бы B принадлежало M, то оно бы мажорировало A, конечно. Но оно не принадлежит.
A - это подмножество M. Я специально подчеркнул, что M состоит не из отрезков, а из множеств отрезков. Семейство A тоже состоит не из отрезков, а из множеств отрезков.
Например, A = { {[0;1], [2;3]}, {[0;1], [2;3], [10;110]} }
Ну и соответственно B для данного конкретного A будет множеством {[0;1], [2;3], [10;110]}. Объединяются не отрезки, а множества отрезков. С самими отрезками ничего не происходит, они как лежали, так и лежат, мы внутрь них не заглядываем. Сами отрезки никак не обрабатываются.
Тут может сложиться ощущение, что я тебя доебываю, но я реально не понимаю.
Давай введем какую-то терминологию, для избежания бардака.
Назовем любое множество попарно непересекающихся отрезков "пунктиром".
М - множество всех подмножеств с пунктирами. А - цепь, значит А линейно упорядочена по включениею, и значит a<b означает, что в b есть все пунктиры a, и еще какие-то. B - множество всех пунктиров, которые принадлежат хоть какому-то A, и без сомнения оно мажорирует A.
Дальше идет аксиома выбора, я как всегда хуй знает как это работает и теряюсь, как представить себе результат, но ок, раз говорят что так, то пусть будет так. Значит существует максимальный элемент S в множестве M. S - как и все остальные элементы множества M, является не пунктиром, а семейством пунктиров, подмножеством множества пунктиров! Если взять два произвольных элемента, то есть два пунктира, то они вполне могут пересекаться между собой, и даже наверняка пересекаются.
Я даже думаю, что можно было сразу говорить, что S=M. Множество всех подмножеств без сомнения является в булеане максимальным элементом.
То есть объясни плиз, как ты из максимального элемента S в множестве всех подмножеств множества пунктиров, выделяешь один, или строишь каким-то образом один, и доказываешь, что он удовлетворяет условиям задачи.
Если человек берется разоблачать обвм другого человека, то у него скорее всего горит.
Я бы например не стал разоблачать твой обвм, потому что мне на него похуй.
>Если человек берется разоблачать обвм другого человека, то у него скорее всего горит.
Не очень понятна логика.
Ну так я, наверное, слишком по-бядляцки выразился. Просто спросить хотел, много ли ты интересного узнал за это время? Ну и да, фраза "мистика всё же довольно тяжёлый труд" звучит нелепо.
Она может звучать нелепо, но это так. Например, осознанные сновидения - это работа, в процессе которой ты затрачиваешь серьезные усилия по удерживанию внимания. Любая работа дисциплинирует человека.
Вопрос о том, какой статус придавать результатам этой работы - это совершенно отдельная тема для беседы, но это сейчас неважно. Результаты занятия математикой это тоже какие-то буковки на бумаге, можно сказать, что они ничего не значат, но если ты просто будешь сидеть и писать какие-то рендомные буквы на бумаге - это не математика. Ты должен действовать по определенным правилам, и это требует от тебя неслабых волевых усилий, которые без сомнения тебя тоже будут дисциплинировать, иначе ты ничего не добьешься.
Ты выше в качестве B брал объединение пунктира, на что я и возражал.
Смотри.
Пунктир - множество попарно непересекающихся отрезков.
Пусть a и b - два пунктира, причём a - подмножество b.
Тогда объединение a и b - пунктир (именно, это b).
Теперь.
M - множество всех пунктиров на прямой.
Они упорядочены по включению, т.е. пунктир a меньше или равен пунктиру b, если все отрезки из a являются отрезками из b.
Цепь в M - множество некоторых пунктиров такое, что для любых двух пунктиров из него один является подмножеством другого.
Объединение любой цепи - пунктир.
Таким образом, для любой цепи пунктиров существует пунктир-мажоранта, а именно объединение этой цепи.
По лемме Цорна, в M существует максимальный пунктир. Т.е. такой пунктир, для которого нельзя предложить больший пунктир. Т.е. в который нельзя добавить отрезок так, чтобы он от этого не перестал быть пунктиром.
Этот максимальный пунктир я явным образом не предъявляю, я просто доказываю, что он существует.
Тут надо просто аккуратно разобраться с определениями.
>>389417
S не равно M. S - пунктир, а M - множество всевозможных пунктиров.
>Объединение любой цепи - пунктир.
Совершенно точно нет, я привел контрпример.
Определим для любого натурального n>3 пунктир A(n) как объединение всех отрезков вида [a+1/n, a+1-1/n], где a пробегает все целые числа. Оно состоит из непересекающихся замкнутых отрезков, периодичных с периодом 1.
Если n<m, то A(n) - меньше или равно A(m), значит это цепь. Но ее объединение не есть пунктир, ее объединение - множество ОТКРЫТЫХ ИНТЕРВАЛОВ! Точнее даже, ее объединение - вся действительная прямая, с выколотыми натуральными точками, поскольку для любого нецелого числа a всегда можно подобрать n, так что 1/n меньше дробной части a, и обратно, 1/n всегда больше нуля, а значит ни одна целая точка не будет принадлежать объединению, поскольку нет ни одного пунктира, которому бы она принадлежала.
Пунктир - это множество отрезков. Пунктир - это не объединение отрезков.
Например, множество {[1;2], [3,4]} - пунктир. А множество [1;2]∪[3,4] - не пунктир.
А, постой, я кажется понял, что ты имеешь в виду. Отрезки добавляются, но не расширяются.
Сейчас, я подумаю.
Бля, ну это пиздец если честно.
Я всегда представлял себе аксиому выбора как эдакий артефакт континуальности.
А тут выходит, что мы счетное множество тоже не можем построить нормально.
Буду думать.
Аксиома выбора нужна. Без неё нельзя доказать, что любое бесконечное множество содержит счётное подмножество, например.
Однако, должен заметить, что все множества, которые мы до этого строили в явном виде, тоже являются максимальными. Если бы на них можно было добавить белый отрезок, значит, существовал бы отрезок, на котором нет белых точек.
Йеп.
Зависит от статуса, который ты придаешь вещам, с которыми сталкиваешься.
Ебать ты гордишься своим решением задачи для 1 курса, уже тредов 20 про него пишешь.
Я очень умный! Задачу для второго курса я тоже решил.
>>381147 (OP)
Это копия, сохраненная 6 января 2017 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.